1. Home
  2. Algebra i for the community
  3. Chapter 1: introduction to real
  4. Chapter 1 part a
  5. Real number line

1.1 Real number line  (Page 3/2)

<< Chapter < Page
  Algebra i for the community     Page 1 / 2
Chapter >> Page >
This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr. The symbols, notations, and properties of numbers that form the basis of algebra, as well as exponents and the rules of exponents, are introduced in this chapter. Each property of real numbers and the rules of exponents are expressed both symbolically and literally. Literal explanations are included because symbolic explanations alone may be difficult for a student to interpret.Objectives of this module: be familiar with the real number line and the real numbers, understand the ordering of the real numbers.

Overview

  • The Real Number Line
  • The Real Numbers
  • Ordering the Real Numbers

The real number line

Real number line

In our study of algebra, we will use several collections of numbers. The real number line allows us to visually display the numbers in which we are interested.

A line is composed of infinitely many points. To each point we can associate a unique number, and with each number we can associate a particular point.

Coordinate

The number associated with a point on the number line is called the coordinate of the point.

Graph

The point on a line that is associated with a particular number is called the graph of that number.

We construct the real number line as follows:

    Construction of the real number line

  1. Draw a horizontal line.

    A horizontal line with arrows on both the ends.
  2. Choose any point on the line and label it 0. This point is called the origin .

    A horizontal line with arrows on both the ends, and a mark labeled as zero.
  3. Choose a convenient length. This length is called "1 unit." Starting at 0, mark this length off in both directions, being careful to have the lengths look like they are about the same.

    A horizontal line with arrows on both the ends, and a mark labeled as zero. There are equidistant marks on both sides of zero.

    We now define a real number.

Real number

A real number is any number that is the coordinate of a point on the real number line.

Positive and negative real numbers

The collection of these infinitely many numbers is called the collection of real numbers . The real numbers whose graphs are to the right of 0 are called the positive real numbers . The real numbers whose graphs appear to the left of 0 are called the negative real numbers .
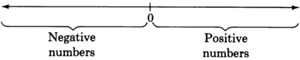
The real numbers having graphs on the right side of the origin are positive numbers, and those having graphs on the left side of the origin are negative numbers.

The number 0 is neither positive nor negative.

The real numbers

The collection of real numbers has many subcollections. The subcollections that are of most interest to us are listed below along with their notations and graphs.

Natural numbers

The natural numbers ( N ) :    { 1 ,   2 , 3 ,   … }

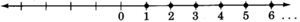
Graphs of natural numbers one to six plotted on a number line. The numberline has arrows on each sides, and is labeled from zero to six in increments of one. There are three dots after six indicating that the graph continues indefinitely.

Whole numbers

The whole numbers ( W ) :    { 0 ,   1 ,   2 , 3 ,   … }

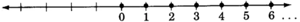
Graphs of whole numbers zero to six plotted on a number line. The number line has arrows on each side, and is labeled from zero to six in increments of one. There are three dots after six indicating that the graph continues indefinitely.

Notice that every natural number is a whole number.

Integers

The integers ( Z ) :    { … ,   − 3 , −   2 , − 1 , 0 , 1 ,   2 ,   3 ,   … }

Graphs of integers negative five to five plotted on a number line. The number line has arrows on each side, and is labeled from negative five to five in increments of one. There are three dots after five indicating that the graph continues indefinitely.

Notice that every whole number is an integer.

Rational numbers

The rational numbers ( Q ) : Rational numbers are real numbers that can be written in the form a / b , where a and b are integers, and b ≠ 0 .

Fractions

Rational numbers are commonly called fractions.

Division by 1

Since b can equal 1, every integer is a rational number: a 1 = a .

Division by 0

Recall that 10 / 2 = 5 since 2 ⋅ 5 = 10 . However, if 10 / 0 = x , then 0 ⋅ x = 10 . But 0 ⋅ x = 0 , not 10. This suggests that no quotient exists.

Now consider 0 / 0 = x . If 0 / 0 = x , then 0 ⋅ x = 0 . But this means that x could be any number, that is, 0 / 0 = 4 since 0 ⋅ 4 = 0 , or 0 / 0 = 28 since 0 ⋅ 28 = 0 . This suggests that the quotient is indeterminant.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra i for the community college. OpenStax CNX. Dec 19, 2014 Download for free at http://legacy.cnx.org/content/col11598/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra i for the community college' conversation and receive update notifications?

Ask