1.1 Real number line (Page 2/2)

Algebra i for the community Page 2 / 2

$x / 0$ Is undefined or indeterminant

Division by 0 is undefined or indeterminant.

Do not divide by 0.

Rational numbers have decimal representations that either terminate or do not terminate but contain a repeating block of digits. Some examples are:

$\begin{matrix} \underset{Terminating}{\underset{︸}{\frac{3}{4} = 0.75}} & \underset{Nonterminating, but repeating }{\underset{︸}{\frac{15}{11} = 1.36363636 \dots}} \end{matrix}$

Some rational numbers are graphed below.

Irrational numbers

The irrational numbers

(I r)

: Irrational numbers are numbers that cannot be written as the quotient of two integers. They are numbers whose decimal representations are nonterminating and nonrepeating. Some examples are

$\begin{matrix} 4.01001000100001 \dots & π = 3.1415927 \dots \end{matrix}$

Notice that the collections of rational numbers and irrational numbers have no numbers in common.

When graphed on the number line, the rational and irrational numbers account for every point on the number line. Thus each point on the number line has a coordinate that is either a rational or an irrational number.

In summary, we have

Sample set a

The summaray chart illustrates that

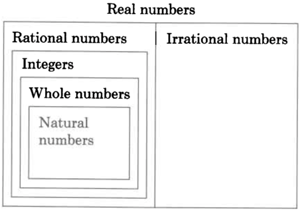
Every natural number is a real number.

Every whole number is a real number.

No integer is an irrational number.

Practice set a

Is every natural number a whole number?

yes

Is every whole number an integer?

yes

Is every integer a rational number?

yes

Is every rational number a real number?

yes

Is every integer a natural number?

Is there an integer that is a natural number?

yes

Ordering the real numbers

A real number

b

is said to be greater than a real number

a

, denoted

b > a

, if the graph of

b

is to the right of the graph of

a

on the number line.

Sample set b

As we would expect, $5 > 2$ since 5 is to the right of 2 on the number line. Also, $- 2 > - 5$ since $- 2$ is to the right of $- 5$ on the number line.

Practice set b

Are all positive numbers greater than 0?

yes

Are all positive numbers greater than all negative numbers?

yes

Is 0 greater than all negative numbers?

yes

Is there a largest positive number? Is there a smallest negative number?

no, no

How many real numbers are there? How many real numbers are there between 0 and 1?

infinitely many, infinitely many

Sample set c

What integers can replace $x$ so that the following statement is true?

$- 4 \leq x < 2$

This statement indicates that the number represented by $x$ is between $- 4$ and 2. Specifically, $- 4$ is less than or equal to $x$ , and at the same time, $x$ is strictly less than 2. This statement is an example of a compound inequality.

The integers are $- 4, - 3, - 2, - 1, 0, 1$ .

Draw a number line that extends from $- 3$ to 7. Place points at all whole numbers between and including $- 2$ and 6.

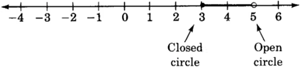
Draw a number line that extends from $- 4$ to 6 and place points at all real numbers greater than or equal to 3 but strictly less than 5.

Graphs of whole numbers between and including negative two and six plotted on a number line. The number line has arrows on each side, and is labeled from negative three to seven in increments of one. Negative two and negative one are not whole numbers, therefore they are not included in the graph.

It is customary to use a closed circle to indicate that a point is included in the graph and an open circle to indicate that a point is not included.

A number line with arrows on each end, and labeled from negative four to six in increments of one. There is a closed circle at three, and an open circle at five. These two circles are connected by a black line.

Practice set c

What whole numbers can replace $x$ so that the following statement is true?

$- 3 \leq x < 3$

0, 1, 2

Draw a number line that extends from $- 5$ to 3 and place points at all numbers greater than or equal to $- 4$ but strictly less than 2.

Exercises

For the following problems, next to each real number, note all collections to which it belongs by writing $N$ for natural numbers, $W$ for whole numbers, $Z$ for integers, $Q$ for rational numbers, $I r$ for irrational numbers, and $R$ for real numbers. Some numbers may require more than one letter.

$\frac{1}{2}$

$Q, R$

$- 12$

$W, Z, Q, R$

$- 24 \frac{7}{8}$

$86.3333 \dots$

$Q, R$

$49.125125125 \dots$

$- 15.07$

$Q, R$

For the following problems, draw a number line that extends from $- 3$ to 3. Locate each real number on the number line by placing a point (closed circle) at its approximate location.

$1 \frac{1}{2}$

$- 2$

$- \frac{1}{8}$

Is 0 a positive number, negative number, neither, or both?

neither

An integer is an even integer if it can be divided by 2 without a remainder; otherwise the number is odd. Draw a number line that extends from $- 5$ to 5 and place points at all negative even integers and at all positive odd integers.

Draw a number line that extends from $- 5$ to 5. Place points at all integers strictly greater than $- 3$ but strictly less than 4.

A number line with arrows on each side, labeled from negative five to five in increments of one. The graphs of the integers negative two to three are plotted on the number line.

For the following problems, draw a number line that extends from $- 5$ to 5. Place points at all real numbers between and including each pair of numbers.

$- 5$ and $- 2$

$- 3$ and 4

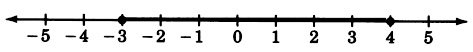
A number line with arrows on each end, labeled from negative five to five in increments of one. There are closed circles at negative three and four. These two circles are connected by a black line.

$- 4$ and 0

Draw a number line that extends from $- 5$ to 5. Is it possible to locate any numbers that are strictly greater than 3 but also strictly less than $- 2$ ?

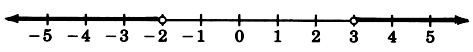A number line with arrows on each end, labeled from negative five to five, in increments of one. There are open circles at negative two and three with a dark shaded arrow to the left of negative two and right of three. ; no

For the pairs of real numbers shown in the following problems, write the appropriate relation symbol $(<, >, =)$ in place of the $*$ .

$- 5 * - 1$

$- 3 * 0$

$<$

$- 4 * 7$

$6 * - 1$

$>$

$- \frac{1}{4} * - \frac{3}{4}$

Is there a largest real number? If so, what is it?

Is there a largest integer? If so, what is it?

Is there a largest two-digit integer? If so, what is it?

Is there a smallest integer? If so, what is it?

Is there a smallest whole number? If so, what is it?

yes, 0

For the following problems, what numbers can replace $x$ so that the following statements are true?

$\begin{matrix} - 1 \leq x \leq 5 & x an integer \end{matrix}$

$\begin{matrix} - 7 < x < - 1, & x an integer \end{matrix}$

$- 6, - 5, - 4, - 3, - 2$

$\begin{matrix} - 3 \leq x \leq 2, & x a natural number \end{matrix}$

$\begin{matrix} - 15 < x \leq - 1, & x a natural number \end{matrix}$

There are no natural numbers between −15 and −1.

$\begin{matrix} - 5 \leq x < 5, & x a whole number \end{matrix}$

The temperature in the desert today was ninety-five degrees. Represent this temperature by a rational number.

${(\frac{95}{1})}^{°}$

The temperature today in Colorado Springs was eight degrees below zero. Represent this temperature with a real number.

Is every integer a rational number?

Yes, every integer is a rational number.

Is every rational number an integer?

Can two rational numbers be added together to yield an integer? If so, give an example.

Yes. $\frac{1}{2} + \frac{1}{2} = 1 or 1 + 1 = 2$

For the following problems, on the number line, how many units (intervals) are there between?

0 and 2?

$- 5$ and 0?

5 units

0 and 6?

$- 8$ and 0?

8 units

$- 3$ and 4?

$m$ and $n$ , $m > n$ ?

$m - n units$

$- a$ and $- b$ , $- b > - a$ ?

Exercises for review

( [link] ) Find the value of $6 + 3 (15 - 8) - 4$ .

( [link] ) Find the value of $5 (8 - 6) + 3 (5 + 2 \cdot 3)$ .

( [link] ) Are the statements $y < 4$ and $y \geq 4$ the same or different?

different

( [link] ) Use algebraic notation to write the statement "six times a number is less than or equal to eleven."

( [link] ) Is the statement $8 (15 - 3 \cdot 4) - 3 \cdot 7 \geq 3$ true or false?

true

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra i for the community college. OpenStax CNX. Dec 19, 2014 Download for free at http://legacy.cnx.org/content/col11598/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra i for the community college' conversation and receive update notifications?

Ask

©flickr: Justin	Music Appreciation Final Practice By Madison Christian Start Exam
	14 AP 14 Brain Cranial Nerves Essay By OpenStax Start Flashcards
	3 Physiotherapy Flashcards Set 3 By Rhodes Start Flashcards
	Art History ARTH209 20th Century By Rebecca Butterfield Start Quiz
	12 Neuroanatomy 12 The Basal Ganglia By Stephen Voron Start Quiz
©flickr: eLife	Mycobacterial Infections (Mandell 8th Ch 251-254) By Cath Yu Start Quiz
	20 AP Key Terms 20 Blood Vessels Circulation By OpenStax Start Key Terms
	College physics for ap® courses By OpenStax Read Online Course
	7 AP 07 Axial Skeleton MCQ By OpenStax Start Quiz
	Biology Exam 2 By Vanessa Soledad Start Exam

1.1 Real number line (Page 2/2)

x / 0 Is undefined or indeterminant

Irrational numbers

Sample set a

Practice set a

Ordering the real numbers

Ordering the real numbers

Sample set b

Practice set b

Sample set c

Practice set c

Exercises

Exercises for review

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

$x / 0$ Is undefined or indeterminant