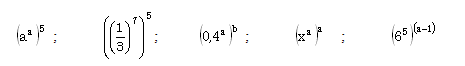Wiskunde
Graad 9
Getalle
Module 2
Maak wiskunde makliker met eksponente
KLASWERK
Onthou jy nog hoe eksponente werk? Skryf neer wat “drie tot die mag sewe” beteken. Wat is die grondtal? Wat is die eksponent? Kan jy mooi verduidelik wat ’n mag is?
Hierdie deel het baie voorbeelde met getalle; gebruik jou sakrekenaar om hulle uit te werk sodat jy vertroue in die metodes kan ontwikkel.
1. DEFINISIE
2
3 = 2 × 2 × 2 en
a
4 =
a ×
a ×
a ×
a en
b ×
b ×
b =
b
3
ook
(
a+
b )
3 = (
a +
b ) × (
a +
b ) × (
a +
b ) en
2
3
4
=
2
3
×
2
3
×
2
3
×
2
3
size 12{ left ( { {2} over {3} } right ) rSup { size 8{4} } = left ( { {2} over {3} } right ) times left ( { {2} over {3} } right ) times left ( { {2} over {3} } right ) times left ( { {2} over {3} } right )} {}
1.1 Skryf die volgende uitdrukkings in uitgebreide vorm:
4
3 (
p +2)
5
a
1 (0,5)
7
b
2 ×
b
3
1.2 Skryf hierdie uitdrukkings as magte:
7 × 7 × 7 × 7
y ×
y ×
y ×
y ×
y –2 × –2 × –2 (
x +
y ) × (
x +
y ) ×
(x +
y ) × (
x +
y )
1.3 Antwoord sonder om dit uit te werk: Is (–7)
6 dieselfde as –7
6 ?
Gebruik nou ’n sakrekenaar en kyk of die twee waardes dieselfde is.
Vergelyk ook die volgende pare deur eers te raai wat die antwoord gaan wees, en dan met jou sakrekenaar te kyk hoe goed jy geskat het.
–5
2 en (–5)
2 –12
5 en (–12)
5 –1
3 en (–1)
3
Jy behoort nou ’n goeie idee te hê hoe hakies antwoorde beïnvloed – skryf dit neer sodat jy dit sal onthou en in die toekoms kan gebruik wanneer die probleme moeiliker word.
Ons som hierdie deel op in ’n definisie:
a
r =
a ×
a ×
a ×
a × . . . (daar moet
r
a ’s wees, en
r moet ’n natuurlike getal wees)
Van nou af moet jy die belangrikste magte begin memoriseer:
2
2 = 4; 2
3 = 8; 2
4 = 16; ens. 3
2 = 9; 3
3 = 27; 3
4 = 81; ens. 4
2 = 16; 4
3 = 64; ens.
Die meeste eksponentsomme moet sonder ’n sakrekenaar gedoen word.
2 VERMENIGVULDIGING
Onthou jy nog dat
g
3 ×
g
8 =
g
11 ? Kernwoorde:
vermenigvuldig ;
dieselfde grondtal
2.1 Vereenvoudig: (moenie uitgebreide vorm gebruik nie).
7
7 × 7
7 (–2)
4 × (–2)
13 ( ½ )
1 × ( ½ )
2 × ( ½ )
3 (
a+b )
a × (
a+b )
b
Ons vermenigvuldig magte met enerse grondtalle volgens hierdie reël:
a
x ×
a
y =
a
x+y
ook
=
a
x
a
y
=
a
y
a
x
a
x
+
y
size 12{ size 11{a rSup { size 8{ size 7{x+y}} } } size 12{ {}=}a rSup { size 8{x} } size 12{ times }a rSup { size 8{y} } size 12{ {}=}a rSup { size 8{y} } size 12{ times }a rSup { size 8{x} } } {} , bv.
8
14
=
8
4
×
8
10
size 12{8 rSup { size 8{"14"} } =8 rSup { size 8{4} } times 8 rSup { size 8{"10"} } } {}
3. DELING
4
6
4
2
=
4
6
−
2
=
4
4
size 12{ { {4 rSup { size 8{6} } } over {4 rSup { size 8{2} } } } =4 rSup { size 8{6 - 2} } =4 rSup { size 8{4} } } {} is hoe dit werk. Kernwoorde:
deel ;
dieselfde grondtal
3.1 Probeer hierdie:
a
6
a
y
size 12{ { { size 11{a rSup { size 8{6} } }} over { size 12{a rSup { size 8{y} } } } } } {}
3
23
3
21
size 12{ { {3 rSup { size 8{"23"} } } over {3 rSup { size 8{"21"} } } } } {}
a
+
b
p
a
+
b
12
size 12{ { { left ( size 11{a+b} right ) rSup { size 8{p} } } over { size 12{ left (a+b right ) rSup { size 8{"12"} } } } } } {}
a
7
a
7
size 12{ { { size 11{a rSup { size 8{7} } }} over { size 12{a rSup { size 8{7} } } } } } {}
Die reël wat ons gebruik vir deling van magte is:
a
x
a
y
=
a
x
−
y
size 12{ { { size 11{a rSup { size 8{x} } }} over { size 12{a rSup { size 8{y} } } } } size 12{ {}=}a rSup { size 8{x - y} } } {} .
Ook
a
x
−
y
=
a
x
a
y
size 12{ size 11{a rSup { size 8{x - y} } } size 12{ {}= { {a rSup { size 8{x} } } over { size 12{a rSup { size 8{y} } } } } }} {} , bv.
a
7
=
a
20
a
13
size 12{ size 11{a rSup { size 8{7} } } size 12{ {}= { {a rSup { size 8{"20"} } } over { size 12{a rSup { size 8{"13"} } } } } }} {}
4. VERHEFFING VAN ’n MAG TOT ’n MAG
bv.
3
2
4
size 12{ left (3 rSup { size 8{2} } right ) rSup { size 8{4} } } {} =
3
2
×
4
size 12{3 rSup { size 8{2 times 4} } } {} =
3
8
size 12{3 rSup { size 8{8} } } {} .
4.1 Doen die volgende:
Die reël werk so:
a
x
y
=
a
xy
size 12{ left (a rSup { size 8{x} } right ) rSup { size 8{y} } =a rSup { size 8{ ital "xy"} } } {}
ook
a
xy
=
a
x
y
=
a
y
x
size 12{ size 11{a rSup { size 8{ bold "xy"} } } size 12{ {}= left (a rSup { size 8{x} } right ) rSup { size 8{y} } } size 12{ {}= left (a rSup { size 8{y} } right ) rSup { size 8{x} } }} {} , bv.
6
18
=
6
6
3
size 12{6 rSup { size 8{"18"} } = left (6 rSup { size 8{6} } right ) rSup { size 8{3} } } {}
5. DIE MAG VAN ’n PRODUK
(2
a )
3 = (2
a ) × (2
a ) × (2
a ) = 2 ×
a × 2 ×
a × 2 ×
a = 2 × 2 × 2 ×
a ×
a ×
a = 8
a
3
Dit word gewoonlik in twee stappe gedoen, nl.: (2
a )
3 = 2
3 ×
a
3 = 8
a
3
5.1 Doen self hierdie: (4
x )
2 (
ab )
6 (3 × 2)
4 ( ½
x )
2 (
a
2
b
3 )
2
Dis duidelik dat die eksponent aan elke faktor in die hakies behoort.
Hier is die reël: (
ab )
x =
a
x
b
x
ook
a
p
b
p
=
ab
b
size 12{ size 11{a rSup { size 8{p} } } size 12{ times }b rSup { size 8{p} } size 12{ {}= left ( bold "ab" right ) rSup { size 8{b} } }} {} bv.
14
3
=
2
×
7
3
=
2
3
7
3
size 12{"14" rSup { size 8{3} } = left (2 times 7 right ) rSup { size 8{3} } =2 rSup { size 8{3} } 7 rSup { size 8{3} } } {}
en
3
2
×
4
2
=
3
×
4
2
=
12
2
size 12{3 rSup { size 8{2} } times 4 rSup { size 8{2} } = left (3 times 4 right ) rSup { size 8{2} } ="12" rSup { size 8{2} } } {}
6. DIE MAG VAN ’n BREUK
Dis baie dieselfde as die mag van ’n produk.
a
b
3
=
a
3
b
3
size 12{ left ( { { size 11{a}} over { size 11{b}} } right ) rSup { size 8{3} } size 12{ {}= { {a rSup { size 8{3} } } over { size 12{b rSup { size 8{3} } } } } }} {}
6.1 Doen hierdie, maar wees versigtig:
2
3
p
size 12{ left ( { {2} over {3} } right ) rSup { size 8{p} } } {}
−
2
2
3
size 12{ left ( { { left ( - 2 right )} over {2} } right ) rSup { size 8{3} } } {}
x
2
y
3
2
size 12{ left ( { { size 11{x rSup { size 8{2} } }} over { size 12{y rSup { size 8{3} } } } } right ) rSup { size 8{2} } } {}
a
−
x
b
−
y
−
2
size 12{ left ( { { size 11{a rSup { size 8{ - x} } }} over { size 12{b rSup { size 8{ - y} } } } } right ) rSup { size 8{ - 2} } } {}
Weer behoort die eksponent aan beide die teller
en die noemer.
Die reël:
a
b
m
=
a
m
b
m
size 12{ left ( { { size 11{a}} over { size 11{b}} } right ) rSup { size 8{m} } size 12{ {}= { {a rSup { size 8{m} } } over { size 12{b rSup { size 8{m} } } } } }} {}
en
a
m
b
m
=
a
b
m
size 12{ { { size 11{a rSup { size 8{m} } }} over { size 12{b rSup { size 8{m} } } } } size 12{ {}= left ( { {a} over { size 12{b} } } right ) rSup { size 8{m} } }} {} bv.
2
3
3
=
2
3
3
3
=
8
27
size 12{ left ( { {2} over {3} } right ) rSup { size 8{3} } = { {2 rSup { size 8{3} } } over {3 rSup { size 8{3} } } } = { {8} over {"27"} } } {}
en
a
2x
b
x
=
a
2
x
b
x
=
a
2
b
x
size 12{ { { size 11{a rSup { size 8{2x} } }} over { size 12{b rSup { size 8{x} } } } } = { { left ( size 11{a rSup { size 8{2} } } right ) rSup { size 8{x} } } over { size 12{b rSup { size 8{x} } } } } size 12{ {}= left ( { {a rSup { size 8{2} } } over { size 12{b} } } right ) rSup { size 8{x} } }} {}
einde van KLASWERK
TUTORIAAL
Pas hierdie reëls saam toe om die volgende uitdrukkings te vereenvoudig — sonder ’n sakrekenaar.
1.
a
5
a
7
a
a
8
size 12{ { { size 11{a rSup { size 8{5} } } size 12{ times }a rSup { size 8{7} } } over { size 12{a size 12{ times }a rSup { size 8{8} } } } } } {}
2.
x
3
y
4
x
2
y
5
x
4
y
8
size 12{ { { size 11{x rSup { size 8{3} } } size 12{ times }y rSup { size 8{4} } size 12{ times }x rSup { size 8{2} } y rSup { size 8{5} } } over { size 12{x rSup { size 8{4} } y rSup { size 8{8} } } } } } {}
3.
a
2
b
3
c
2
ac
2
2
bc
2
size 12{ left ( size 11{a rSup { size 8{2} } b rSup { size 8{3} } c} right ) rSup { size 8{2} } size 12{ times left ( bold "ac" rSup { size 8{2} } right ) rSup { size 8{2} } } size 12{ times left ( bold "bc" right ) rSup { size 8{2} } }} {}
4.
a
3
b
2
a
3
a
b
5
b
4
ab
3
size 12{ size 11{a rSup { size 8{3} } } size 12{ times }b rSup { size 8{2} } size 12{ times { {a rSup { size 8{3} } } over { size 12{a} } } } size 12{ times { {b rSup { size 8{5} } } over { size 12{b rSup { size 8{4} } } } } } size 12{ times left ( bold "ab" right ) rSup { size 8{3} } }} {}
5.
2
xy
×
2
x
2
y
4
2
x
2
y
3
2
xy
3
size 12{ left (2 size 11{ bold "xy"} right ) times left (2 size 11{x rSup { size 8{2} } y rSup { size 8{4} } } right ) rSup { size 8{2} } size 12{ times left ( { { left (x rSup { size 8{2} } y right ) rSup { size 8{3} } } over { size 12{ left (2 bold "xy" right ) rSup { size 8{3} } } } } right )}} {}
6.
2
3
×
2
2
×
2
7
8
×
4
×
8
×
2
×
8
size 12{ { {2 rSup { size 8{3} } times 2 rSup { size 8{2} } times 2 rSup { size 8{7} } } over {8 times 4 times 8 times 2 times 8} } } {}
einde van TUTORIAAL
Nog ’n paar reëls
KLASWERK
1 Beskou hierdie geval:
=
a
5
−
3
=
a
2
a
5
a
3
size 12{ { { size 11{a rSup { size 8{5} } }} over { size 12{a rSup { size 8{3} } } } } size 12{ {}=}a rSup { size 8{5 - 3} } size 12{ {}=}a rSup { size 8{2} } } {}