| << Chapter < Page | Chapter >> Page > |
Chapter 2. Solid State of Matter.
Section.2.5. Bohr Model of Hydrogen Atom.
According to Maxwell’s Equation an accelerated electron must give off radiation and lose energy. An electron in an atom in a circular orbit is continuously accelerated towards the center. The acceleration towards the center is:
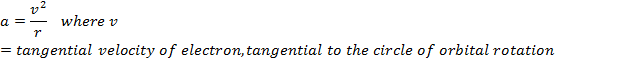

This centripetal force is supplied by the electrostatic force of attraction by the nucleus of the Atom given by the following expression:
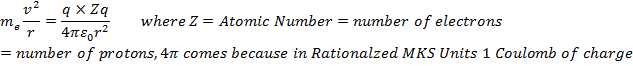
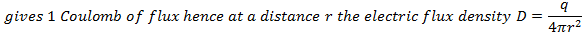
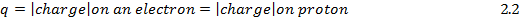
Therefore:

A circularly orbiting electron is continuously being accelerated towards the center hence it should be giving of SYNCHROTRON Radiation. Synchrotron radiation has the same frequency as the rate at which electron is orbiting the nucleus of the Atom. Infact this principle is being utilized in modern day Synchrotrons and Betatrons. If this is to occur then electron must spiral into the nucleus and atom must collapse. But all around us the atoms are stable. Hence Bohr made the following Postulates:
Postulate 1. Electrons are in Stationary States. There are some discrete energy states in which electrons are permitted to stay.
Postulate 2. In the stationary states:
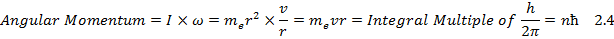
In a few years de Broglie in France gave his hypothesis of matter wave and that:

Combining Bohr’s Law (2.4) and de Broglie hypothesis (2.5) we get the following:

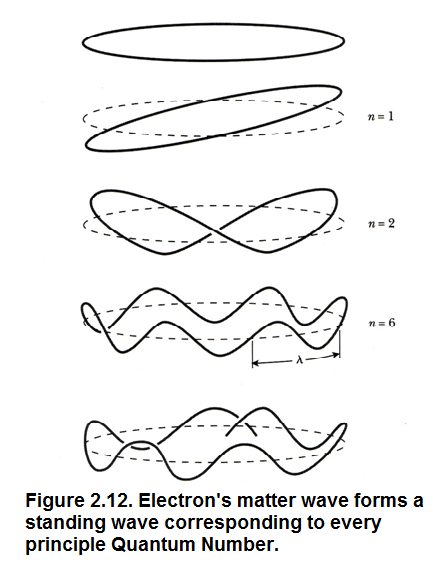
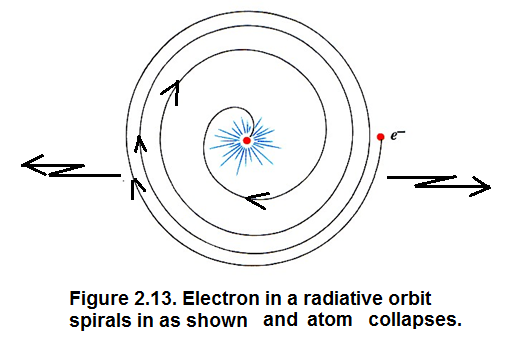
Equation (2.6) implies that only the electrons which form a standing wave along their respective orbital paths as shown in Figure 2.12. are permitted to stay in stationary orbits. If the electron does not form a standing wave it starts radiating and it spirals in as shown in Figure 2.13.
From (2.4) squaring both sides we get:

Multiplying both sides by the mass of electron we get:

Both (2.3) and (2.8) give twice the Kinetic Energy of the orbiting electron. In (2.3) the KE has been obtained from Newtonian Mechanics consideration whereas from Bohr’s postulate (2.8) has been obtained. But the two are equal. Based on this equality we obtain:

Rearranging the terms we obtain the radius of the orbits as follows:
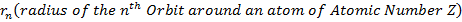
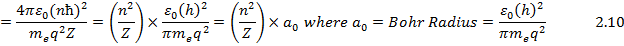
Calculating the Bohr Radius we get : a 0 = 52.9459 picometer(pm).
Here we have taken the Universal Constants and electron charge and mass as follows:
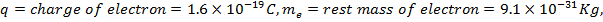
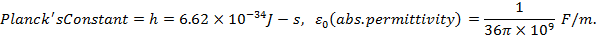
According to Quantum Mechanics, the maximum probability density occurs at Bohr Radius but the total probability within a sphere of Bohr Radius is less than 65%.
Section 2.5.1. Total Energy of Electron in n th Orbit of an Atom of Atomic Number Z.
Total Energy TE is given as follows:
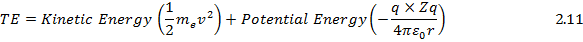
From (2.3) we find that 2×KE = magnitude of PE hence TE simplifies to:

Substituting the nth Orbit Radius (r n ) as given in (2.10) we get TE as follows:
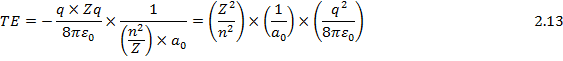
From (2.10) and (2.13) gives the orbital radius and the corresponding energy for any atom of Atomic Number Z.
Section 2.5.2. Calculation of the orbital radii and Total Energy of different principle Orbits of Hydrogen Atom.

Notification Switch
Would you like to follow the 'Electrical and electronic materials science' conversation and receive update notifications?