| << Chapter < Page | Chapter >> Page > |
We use (2.10) and (2.13) to determine the orbital radii and total energy of the discrete energy states of Hydrogen. Here Z=1 is taken since H atom has 1 electron and 1 proton. In (2.13) the results are obtained in Joules. To obtain results in eV we must divide Joules by (qC×1V). The results of calculations is given in Table 2.13.
Table 2.13.Radii and total Energy of Hydrogen Atom Principal electronic Orbits.
| (Principal Quantum Number)n | r n (Angstrom) | Total Energy(eV) |
|---|---|---|
| 1 | 0.529 | -13.6 |
| 2 | 2.12 | -3.4 |
| 3 | 4.76 | -1.5 |
| 4 | 8.47 | -0.85 |
Based on the above Table a correct theoretical basis of the Spectral Lines of Hydrogen Atom was provided by Neil Bohr as explained in Figure 2.14.
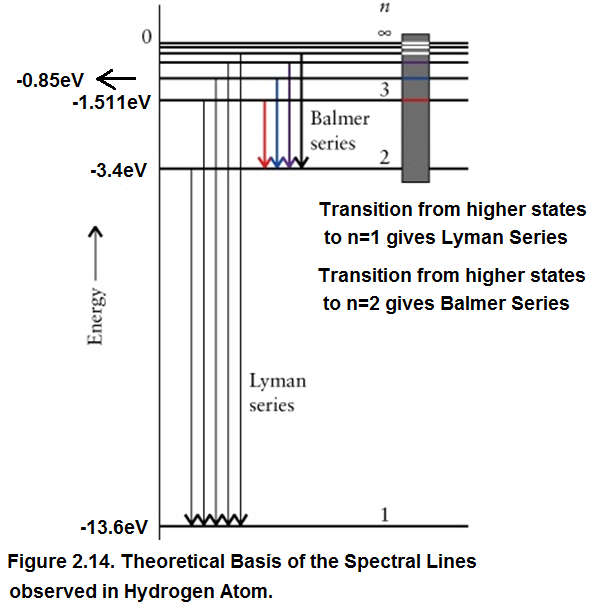
As seen in Figure 2.14:
Transition from higher states to ground state namely n =1 gives Lyman Series.
Transition from higher states to next excited state namely n =2 gives Balmer Series.
Transition from higher states to third excited state namely n =3 gives Paschen Series.
Transition from higher states to fourth excited state namely n =4 gives Brackett Series.
Transition from higher states to fifth excited state namely n =5 gives Pfund Series.
Section 2.5.3. Problems with Bohr Theory.
Bohr’s Model is unable to show that apart from Principal Quantum Numbers(n) there are azimuthial/orbital quantum number ( l ) , magnetic quantum numbers (m) and spin quantum numbers (s).
In 1925, Erwin Schrodinger proposed Wave Mechanics applicable to matter wave.
His proposition was the following:

H is the Hamiltonian Operator which includes KE plus PE operator. The Hamiltonian Operator operating on Matter Wave yields the Eigen Values of Hamiltonian Operation.
This equation was applied to an electron orbiting a proton in a Hydrogen atom. Since it had spherical symmetry hence Spherical Coordinates or Spherical Frame of Reference was adopted. The solution of Schrodinger Equation yielded the three non-relativistic quantum numbers namely:
Principal Quantum Number ‘n’ which gives the quantization of Energy of Orbital Electrons.
Azimuthial/Orbital Quantum Number ‘ l ’ which gives the quantization of the orbital angular momentum L.
Magnetic Quantum Number ‘m’ which gives the quantization of the orientation of L with a special frame of reference Z axis.
(2.14) is non-relativistic equation hence only non-relativistic Quantum Numbers are predicted.
Relativistic treatment yields the Spin Quantum Numbers.
These four Quantum Number have been explained Section 2.4.
Bohr Theory could not be used to determine energies of atoms with more than one electron. It was unable to explain fine structure observed in H atom spectra. It cannot be used to understand bonding in molecules, nor can it be used to calculate energies of even the simplest molecules. Bohr’s model based on classical mechanics, used a quantization restriction on a classical model.
Section 2.5.3. Calculation of Outermost Orbital Radii and Total Energy associated with Outermost Electron in Noble Gases He, Ne, Ar, Kr, Xe and Rn.
Equations (2.10) and (2.13) cannot be directly applied to atoms heavier than Hydrogen. This is because in complex atoms while studying the outermost orbit we have to account for the screening effect of the intervening electron cloud.
The Inert Gases and their electronic configurations are tabulated in Table 2.3
Table 2.3. Shell Structure of Inert Gas Atoms.
| Gas | Z | K-Shell(n=1) | L-Shell(n=2) | M-Shell(n=3) | N-Shell(n=4) | O-Shell(n=5) | P-Shell(n=6) |
|---|---|---|---|---|---|---|---|
| He | 2 | 1s 2 | |||||
| Ne | 10 | 1s 2 | 2s 2 ,2p 6 | ||||
| Ar | 18 | 1s 2 | 2s 2 ,2p 6 | 3s 2 ,3p 6 | |||
| Kr | 36 | 1s 2 | 2s 2 ,2p 6 | 3s 2 ,3p 6 ,3d 10 | 4s 2 ,4p 6 | ||
| Xe | 54 | 1s 2 | 2s 2 ,2p 6 | 3s 2 ,3p 6 ,3d 10 | 4s 2 ,4p 6 ,4d 10 | 5s 2 ,5p 6 | |
| Rn | 86 | 1s 2 | 2s 2 ,2p 6 | 3s 2 ,3p 6 ,3d 10 | 4s 2 ,4p 6 ,4d 10 ,4f 14 | 5s 2 ,5p 6 ,5d 10 | 6s 2 ,6p 6 |
From Table 2.3 it is evident that in Neon, K-shell electrons and L Shell s-orbital electrons will have a screening effect to the extent that p-orbital in L-Shell will experience only the pull of (10-4) protons and screening factor (S) is 4.
In Argon, K-shell , L-Shell and M-Shells s-orbital electrons will have a screening effect to the extent that p-orbital in M-Shell will experience only the pull of (18-12) protons and screening factor (S) is 12.
In Krypton, K- shell, L-Shell, M-Shell and N-Shell s-orbital electrons will have a screening effect to the extent that p-orbital in N-Shell will experience only the pull of (36-30) protons and screening factor (S) is 30.
In Xeon, K-shell, L Shell, M-Shell, N-Shell and O-Shell s-orbital electrons will have a screening effect to the extent that p-orbital in O-Shell will experience only the pull of (54-48) protons and screening factor (S) is 48.
In Radon, K shell, L Shell, M-Shell, N-Shell, O-Shell and P-Shell s-orbital electrons will have a screening effect to the extent that p-orbital in P-Shell will experience only the pull of (86-80) protons and screening factor (S) is 80.
In 1964, J.C.Slater empirically measured the covalent bonds of all the elements and published their outer orbital radii.by the title “Atomic Radii in Crystals” in Journal of Chemical Physics, Volume 41, No.10, pp 3199-3205.
I used these empirical values of atomic radii and the modified formula for (2.10) namely:
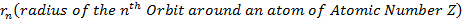

Using the empirical values of the radii and using (2.15) I determined the actual screening effect in each case.
The magnitude of the total energy of the outermost orbital electron directly gives the First Ionization Energy and this has been experimentally measured by .
Table 2.4.Empirical Radii(R), Z, calculated S* , experimentally measured First Ionization Energy of the 6 Inert Gases.
| Inert Gas | R(pm) | Z | S* | n(P.Q.N of outermost orbit) | First Ionization Energy(eV)† |
|---|---|---|---|---|---|
| He | 31 | 2 | 0.292068 | 1 | 24.8 |
| Ne | 38 | 10 | 4.42675 | 2 | 21.5 |
| Ar | 71 | 18 | 11.2885 | 3 | 16.0 |
| Kr | 88 | 36 | 26.3735 | 4 | 14.0 |
| Xe | 108 | 54 | 41.744 | 5 | 12.0 |
| Rn | 120 | 86 | 70.1162 | 6 | 11.0 |
S*- calculated value of Screening effect by me.
E*- calculated value of total energy of the outermost orbital electron.
P.Q.N- Principal Quantum Number.
†Experimentally determined by Greenwood(reference not available)

Notification Switch
Would you like to follow the 'Electrical and electronic materials science' conversation and receive update notifications?