| << Chapter < Page | Chapter >> Page > |
To see the continuous scaling function and wavelet moments for these systems, [link] shows both the continuous and discrete moments for the length-6 and 8 coiflet systems. Noticethe zero moment for length-8. The length-14, 20, and 26 systems also have the “extra" zero scaling moment just after the first nonzero moment.This always occurs for length- coiflets.
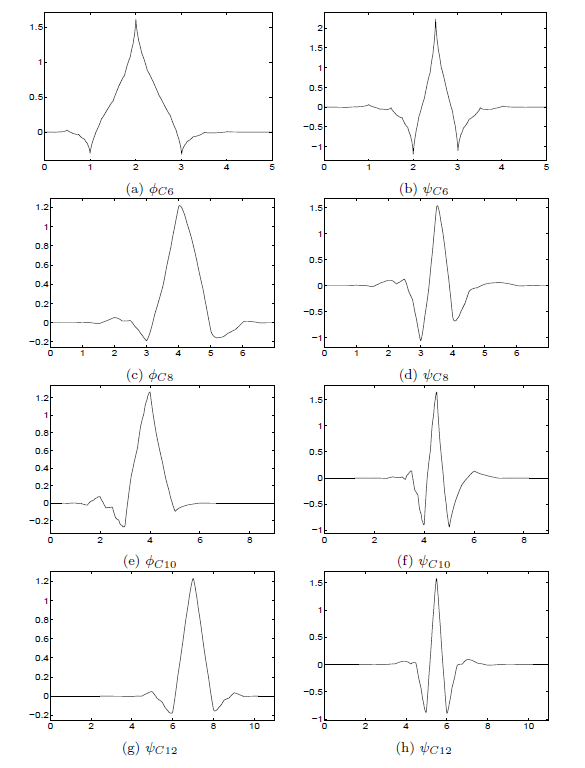
[link] shows the length-6, 8, 10, and 12 coiflet scaling functions and wavelets . Notice their approximate symmetry and compare this to Daubechies' classical wavelet systems and her moresymmetric ones achieved by using the different factorization mentioned in [link] and shown in [link] . The difference between these systems and truly symmetric ones (which requires giving up orthogonality,realness, or finite support) is probably negligible in many applications.
The preceding section shows that Coifman systems do not necessarily have an equal number of scaling function and wavelet moments equal to zero.Lengths have equal numbers of zero scaling function and wavelet moments, but always have even-order “extra" zero scaling function momentslocated after the first nonzero one. Lengths always have an “extra" zero scaling function moment. Indeed, both will have severaleven-order “extra" zero moments for longer as a result of the relationships illustrated in [link] through [link] . Lengths do not occur for the original definition of a Coifman system if one looks only at the degree with minimum length. If we specify thelength of the coefficient vector, all even lengths become possible, some with the same coiflet degree.
We examine the general Coifman wavelet system defined in [link] and [link] and allow the number of specified zero scaling function and wavelet moments to differ by at most one. That will include all thereported coiflets plus length-10, 16, 22, and . The length-10 was designed by Odegard [link] by setting the number of zero scaling functions to 3 and the number of zero waveletmoment to 2 rather than 2 and 2 for the length-8 or 3 and 3 for the length-12 coiflets. The result in [link] shows that the length-10 design again gives one extra zero scaling function moment whichis two more than the number of zero wavelet moments. This is an even-order moment predicted by [link] and results in a total number of zero moments between that for length-8 and length-12, as one wouldexpect. A similar approach was used to design length-16, 22, and 28.
| Length- , | Degree | ||||
| -1 | 0.224143868042 | 0.129409522551 | 1.414213 | 0 | 0 |
| 0 | 0.836516303737 | 0.482962913144 | 0 | -0.517638 | 1 |
| 1 | 0.482962913144 | -0.836516303737 | 0.189468 | 0.189468 | 2 |
| 2 | -0.129409522551 | 0.224143868042 | -0.776457 | 0.827225 | 3 |
| Length- , | Degree | ||||
| -2 | 0.032128481856 | 0.000233764788 | 1.414213 | 0 | 0 |
| -1 | -0.075539271956 | -0.000549618934 | 0 | 0 | 1 |
| 0 | -0.096935064502 | -0.013550370057 | 0 | 0 | 2 |
| 1 | 0.491549094027 | 0.033777338659 | 0 | 3.031570 | 3 |
| 2 | 0.805141083557 | 0.304413564385 | 0 | 24.674674 | 4 |
| 3 | 0.304413564385 | -0.805141083557 | -14.709025 | 138.980052 | 5 |
| 4 | -0.033777338659 | 0.491549094027 | 64.986095 | 710.373341 | 6 |
| 5 | -0.013550370057 | 0.096935064502 | |||
| 6 | 0.000549618934 | -0.075539271956 | |||
| 7 | 0.000233764788 | 0.032128481856 |

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?