| << Chapter < Page | Chapter >> Page > |
To determine for what signal and filter durations a time- or frequency-domain implementation would be the most efficient, weneed only count the computations required by each. For the time-domain, difference-equation approach, we need . The frequency-domain approach requires three Fourier transforms, eachrequiring computations for a length- FFT, and the multiplication of two spectra( computations). The output-signal-duration-determined length must be at least . Thus, we must compare Exact analytic evaluation of this comparison is quite difficult (we have a transcendental equation to solve). Insight into thiscomparison is best obtained by dividing by . With this manipulation, we are evaluating the number of computations per sample. For any given value of the filter'sorder , the right side, the number of frequency-domain computations, will exceed the left ifthe signal's duration is long enough. However, for filter durations greater than about 10, as long as the input is atleast 10 samples, the frequency-domain approach is faster so long as the FFT's power-of-two constraint is advantageous .
The frequency-domain approach is not yet viable; what will we do when the input signal is infinitely long? Thedifference equation scenario fits perfectly with the envisioned digital filtering structure , but so far we have required the input to have limited duration (so that we could calculateits Fourier transform). The solution to this problem is quite simple: Section the input into frames, filter each, and add theresults together. To section a signal means expressing it as a linear combination of length- non-overlapping "chunks." Because the filter is linear, filtering a sum of terms is equivalent to summing the results offiltering each term.
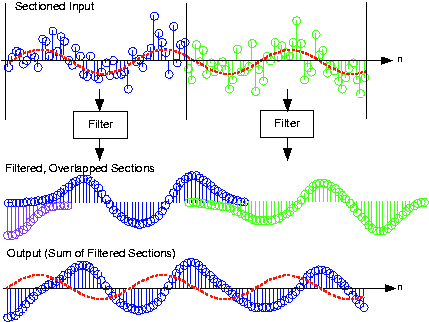
Computational considerations reveal a substantial advantage for a frequency-domain implementation over a time-domain one. The numberof computations for a time-domain implementation essentially remains constant whether we section the input or not. Thus, the number ofcomputations for each output is . In the frequency-domain approach, computation counting changes because we need only compute the filter'sfrequency response once, which amounts to a fixed overhead. We need only compute two DFTs and multiply them to filter a section. Letting denote a section's length, the number of computations for a section amounts to . In addition, we must add the filtered outputs together; the number of terms to add corresponds to the excessduration of the output compared with the input ( ). The frequency-domain approach thus requires computations per output value. For even modest filter orders, the frequency-domain approach is much faster.

Notification Switch
Would you like to follow the 'Discrete-time fourier analysis' conversation and receive update notifications?