| << Chapter < Page | Chapter >> Page > |
Show that as the section length increases, the frequency domain approach becomes increasingly more efficient.
Let denote the input's total duration. The time-domain implementation requires a total of computations, or computations per input value. In the frequency domain, we split the input into sections, each of which requires per input in the section. Because we divide again by to find the number of computations per input value in the entire input, this quantity decreases as increases. For the time-domain implementation, it stays constant.
Note that the choice of section duration is arbitrary. Once thefilter is chosen, we should section so that the required FFT length is precisely a power of two: Choose so that .
Implementing the digital filter shown in the A/D block diagram with a frequency-domain implementation requires some additional signal management not required by time-domainimplementations. Conceptually, a real-time, time-domain filter could accept each sample as it becomes available, calculate thedifference equation, and produce the output value, all in lessthan the sampling interval . Frequency-domain approaches don't operate on asample-by-sample basis; instead, they operate on sections. They filter in real time by producing outputs for the same number of inputs faster than . Because they generally take longer to produce an output section than the sampling interval duration, we mustfilter one section while accepting into memory the next section to be filtered. In programming, the operation of building up sections whilecomputing on previous ones is known as buffering . Buffering can also be used in time-domain filters as well butisn't required.
We want to lowpass filter a signal that contains a sinusoid and a significant amount of noise. The example shown in [link] shows a portion of the noisy signal's waveform. If it weren't for the overlaid sinusoid, discerning the sine wavein the signal is virtually impossible. One of the primary applications of linear filters is noise removal : preserve the signal by matching filter's passband with thesignal's spectrum and greatly reduce all other frequency components that may be present in the noisy signal.
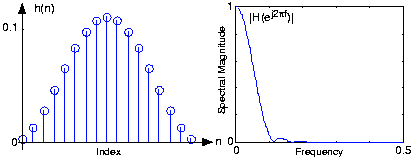
A smart Rice engineer has selected a FIR filter having a unit-sampleresponse corresponding a period-17 sinusoid: , , which makes . Its frequency response (determined by computing the discrete Fourier transform) is shown in [link] . To apply, we can select the length of each section so that the frequency-domain filteringapproach is maximally efficient: Choose the section length so that is a power of two. To use a length-64 FFT, each section must be 48 samples long. Filtering with the difference equationwould require 33 computations per output while the frequency domain requires a little over 16; this frequency-domainimplementation is over twice as fast! [link] shows how frequency-domain filtering works.
We note that the noise has been dramatically reduced, with a sinusoid now clearly visible in the filtered output. Someresidual noise remains because noise components within the filter's passband appear in the output as well as the signal.
Note that when compared to the input signal's sinusoidal component, the output's sinusoidal component seems to bedelayed. What is the source of this delay? Can it be removed?
The delay is not computational delay here--the plot shows the first output value is aligned with the filter's firstinput--although in real systems this is an important consideration. Rather, the delay is due to the filter's phase shift: Aphase-shifted sinusoid is equivalent to a time-delayed one: . All filters have phase shifts. This delay could be removed if the filter introduced no phase shift. Suchfilters do not exist in analog form, but digital ones can be programmed, but not in real time. Doing so would require theoutput to emerge before the input arrives!

Notification Switch
Would you like to follow the 'Discrete-time fourier analysis' conversation and receive update notifications?