| << Chapter < Page | Chapter >> Page > |
A-cây có nút đỉnh là 3 tạo ra chuỗi con abba theo chuỗi dẫn xuất :
S Þ SbAÞ abA Þ abba
Câu hỏi :
?
Các cây dẫn xuất được sinh từ những chuỗi dẫn xuất khác nhau cho cùng một chuỗi nhập có là những cây dẫn xuất khác nhau không ?
ĐỊNH LÝ 5.1 : Nếu G (V, T, P, S) là một văn phạm phi ngữ cảnh thì S * nếu và chỉ nếu có cây dẫn xuất trong văn phạm sinh ra .
Ta chứng minh rằng với biến A bất kỳ, A * nếu và chỉ nếu có một A-cây sinh ra .
Nếu: Giả sử được sinh bởi A-cây, ta chứng minh quy nạp theo số nút trung gian của cây dẫn xuất rằng A *.
Nếu có 1 nút trung gian thì cây phải có dạng như hình sau :
Khi đó X1X2 ... Xn là chuỗi và A là một luật sinh trong P theo định nghĩa cây dẫn xuất.
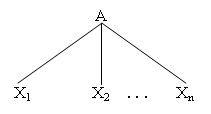
Hình 5.2(a) - A-cây với một nút trong
Giả sử kết quả đúng tới k -1 nút trung gian ( k>1)
Ta chứng minh kết quả cũng đúng với k nút.
Xét được sinh ra bởi A-cây có k nút trung gian. Rõ ràng các nút con của nút gốc không phải tất cả đều là lá, ta gọi chúng từ trái sang phải là X1, X2, ..., Xn thì chắc chắn rằng A X1X2 ... Xn là một luật sinh. Xét nút Xi bất kỳ :
- Nếu Xi không là nút lá thì Xi phải là một biến và Xi - cây con sẽ sinh ra một chuỗi i nào đó.
- Nếu Xi là nút lá, ta đặt i = Xi. Dễ thấy rằng nếu j<i thì các j ở bên trái j, do vậy chuỗi đọc từ lá vẫn có dạng = 12 ... n. Mỗi Xi - cây con phải có ít nút trung gian hơn cây ban đầu, vì thế theo giả thiết quy nạp, với mỗi đỉnh i không phải là lá thì Xi *i.
Vậy A X1X2 ... Xn * 1X2 ... Xn * 12X3 ... Xn * ... * 12 ... n =
Hay ta có A * . Chú ý rằng đây chỉ là một trong nhiều cách dẫn xuất ra .
Chỉ nếu : Ngược lại, giả sử A * ta cần chỉ ra một A - cây sinh ra .
Nếu A * bằng một bước dẫn xuất thì A là một luật sinh trong P và có cây dẫn xuất sinh ra như trong hình trên.
Giả sử kết quả đúng tới k-1 bước dẫn xuất
Xét A * bằng k bước dẫn xuất, gọi bước đầu tiên là A X1X2 ... Xn.
Rõ ràng, một ký hiệu trong phải được dẫn ra từ một biến Xi nào đó. Vì vậy, ta có thể viết = 12 ... n, trong đó mỗi 1 i n thoả mãn :
- i = Xi nếu Xi là ký hiệu kết thúc.
- Xi * i nếu Xi là một biến.
Nếu Xi là biến thì dẫn xuất của i từ Xi phải có ít hơn k bước. Vì vậy, theo giả thiết quy nạp ta có Xi - cây sinh ra i, đặt cây này là Ti
Bây giờ ta dựng A - cây có n lá X1X2 ... Xn. Mỗi Xi không là ký hiệu kết thúc ta thay bằng cây Ti tương ứng. Cuối cùng, ta có cây dẫn xuất sinh ra có dạng như sau :
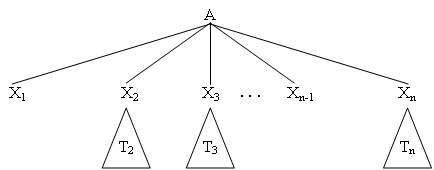
Hình 5.2(b) - A-cây
Thí dụ 5.6 :Xét chuỗi dẫn xuất S * aabbaa cho văn phạm ở Thí dụ 5.4.
Bước đầu tiên trong dẫn xuất đó là S aAS. Theo dõi các bước suy dẫn sau đó, ta thấy biến A được thay bởi SbA, rồi trở thành abA và cuối cùng thành abba, đó chính là kết quả của cây T2 (A - cây). Còn biến S thì được thay bởi a và đó là kết quả của cây T3 (S -cây). Ghép nối lại, ta được cây dẫn xuất mà kết quả là chuỗi aabbaa như dưới đây.
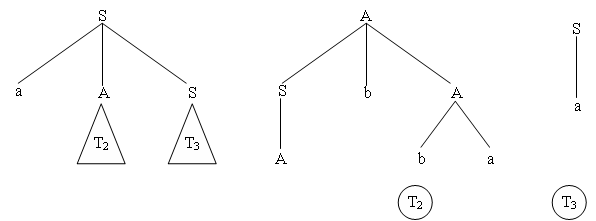
[
Hình 5.3 - Ghép nối các cây dẫn xuất
Nếu tại mỗi bước dẫn xuất, luật sinh được áp dụng vào biến bên trái nhất thì ta gọi đó là dẫn xuất trái nhất (leftmost) hay dẫn xuất trái. Tương tự, nếu biến bên phải nhất được thay thế ở mỗi bước dẫn xuất, đó là dẫn xuất phải nhất (rightmost) hay dẫn xuất phải. Nếu chuỗi w L(G) với CFG G thì w sẽ có ít nhất một cây dẫn xuất ra nó và tương ứng với các cây này, w chỉ có duy nhất một dẫn xuất trái nhất và duy nhất một dẫn xuất phải nhất. Dĩ nhiên, w có thể có nhiều dẫn xuất trái (phải) nhất vì nó có thể có nhiều cây dẫn xuất.

Notification Switch
Would you like to follow the 'Giáo trình tin học lý thuyết' conversation and receive update notifications?