| << Chapter < Page | Chapter >> Page > |
Thí dụ 5.13 : Tìm văn phạm có dạng GNF tương đương văn phạm G sau :
A1 ® A2A1 | A2A3
A2 ® A3A1 | a
A3 ® A2A2 | b
Bước 1 : G thỏa dạng chuẩn CNF sinh ra CFL không chứa
Bước 2 : Ta có V = {A1, A2, ..., A3}
Bước 3 : Thay thế các luật sinh sao cho nếu Ai Aj là một luật sinh thì j>i.
Ta thấy trong tập luật sinh, các luật sinh cho A1 và A2 đã thỏa điều kiện j>i. Chỉ có luật sinh A3 ® A2A2 cần sửa đổi. Áp dụng bổ đề 3 để thay thế luật sinh này, ta có:A3 ® A3A1A2 | aA2
Sau đó, dùng bổ đề 4 để loại bỏ đệ quy trái, ta được tập luật sinh mới có dạng như sau :
A1 ® A2A1 | A2A3
A2 ® A3A1 | a
A3 ® aA2 | b | aA2B | bB
B ® A1A2 | A1A2 B
Bước 4 : Thay thế các Ai -luật sinh về đúng dạng.
Ở bước này, ta có thể thấy tất cả các A3 - luật sinh đã có dạng chuẩn. Tiếp tục, áp dụng bổ đề 3 để thay thế các A3 - luật sinh vào A2, A1, thu được tập luật sinh mới như sau:
A1 ® aA2A1A1 | bA1A1 | aA2BA1A1 | bBA1A1 | aA1|
aA2A1A3 | bA1A3 | aA2BA1A3 | bBA1A3 | aA3
A2 ® aA2A1 | bA1 | aA2BA1| bBA1| a
A3 ® aA2 | b | aA2B | bB
B ® A1A2 | A1A2 B
Bước 5 : Thay thế các Bk - luật sinh về đúng dạng.
B ® aA2A1A1A2 | bA1A1A2 | aA2BA1A1A2 | bBA1A1A2 | aA1A2
| aA2A1A3A2 | bA1A3A2 | aA2BA1A3A2 | bBA1A3A2 | aA3A2
| aA2A1A1A2B | bA1A1A2B | aA2BA1A1A2B | bBA1A1A2B | aA1A2 B
| aA2A1A3A2B | bA1A3A2B | aA2BA1A3A2B | bBA1A3A2B | aA3A2B
Cuối cùng, ta thu được văn phạm có dạng GNF với 39 luật sinh.
Cũng như lớp ngôn ngữ chính quy, có một vài tính chất giúp xác định một ngôn ngữ có thuộc lớp ngôn ngữ phi ngữ cảnh hay không ?
(Dùng chứng minh một ngôn ngữ không là ngôn ngữ phi ngữ cảnh)
Cho L là một CFL bất kỳ, tồn tại một số n chỉ phụ thuộc vào L sao cho nếu z L và | z | n thì ta có thể viết z = uvwxy sao cho:
1) | vx | ³ 1
2) | vwx | n và
3) i ³ 0 : uviwxiy Î L
Chứng minh
Đặt G là văn phạm có dạng chuẩn CHOMSKY sinh L - {}. Chú ý rằng nếu z L(G) và cây dẫn xuất không có đường đi dài hơn i thì chuỗi sinh ra từ văn phạm có độ dài không dài hơn 2 i -1.
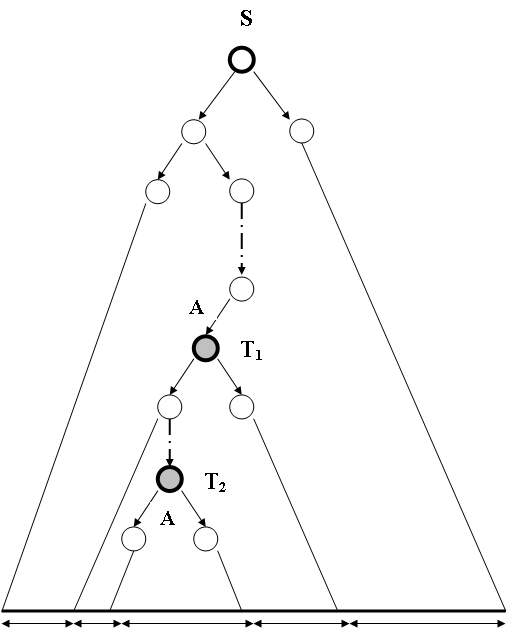
z3 z2 z4
z = u v w x y
Hình 5.5 - Các bước dẫn xuất trong chứng minh Bổ đề bơm
Giả sử G có k biến, ta đặt n = 2k. Nếu z L(G) và | z | n thì | z |>2k-1, vậy có một đường đi nào đó trên cây dẫn xuất có độ dài lớn hơn hoặc bằng k+1. Như vậy đường đi đó sẽ có ít nhất k+2 đỉnh, hay có ít nhất k+1 biến trên đường đi (chỉ có nút lá mới có thể không là biến), suy ra phải có biến xuất hiện hai lần, hơn nữa ta phải có:
1) Có hai đỉnh v1 và v2 có cùng nhãn là A
2) Đỉnh v1 gần gốc hơn v2
3) Phần đường đi từ v1 tới lá có độ dài nhiều nhất là k+1 (đi từ lá lên tới gốc theo đường đi, chỉ có lá mới có thể là ký hiệu kết thúc vì vậy trong k+2 đỉnh đầu tiên phải có ít nhất k+1 biến và phải có ít nhất hai biến trùng nhau)
Xét cây con T1 có đỉnh là v1 biểu diễn dẫn xuất của chuỗi con có độ dài không quá 2k (vì trong cây con T1 không có đường đi nào có độ dài vượt quá k+1). Đặt z1 là chuỗi sinh ra từ cây T1. Ta gọi T2 là một cây con có nút gốc là v2, rõ ràng T2 là cây con của T1. Giả sử T2 sinh ra chuỗi z2 thì ta có thể viết z1 = z3z2z4. Hơn nữa z3 và z4 không thể đồng thời bằng vì luật sinh đầu tiên trong cây dẫn xuất của T1 là A BC với biến B, C nào đó. Cây con T2 phải thuộc vào cây con sinh bởi bút biến B hoặc cây con sinh bởi nút biến C. Ta có :

Notification Switch
Would you like to follow the 'Giáo trình tin học lý thuyết' conversation and receive update notifications?