| << Chapter < Page | Chapter >> Page > |
We need to focus on atoms, so we’ll look only at the spectroscopy of pure elements. Each element has a characteristic spectrum of frequencies. We will focus on the light frequencies which are x-rays and, even more carefully, for each element we will focus on the lowest frequency x-ray which each atom emits. These are given for many of the elements in [link] . The ordering of the elements in [link] is important. We could have listed them alphabetically by name. Instead, we have listed them in their order of increasing relative mass. In the set of elements given here, lithium is the least massive element so it is at the top, then beryllium, and so forth. Note that the x-ray frequency emitted by each atom increases as the masses of the atoms increase moving down [link] . (There is one exception to our order in [link] : Argon is slightly more massive than Potassium, but we have put Argon before Potassium for reasons that we will discuss later.)
| Atomic Number | Element Name | X-ray frequency (10 16 s -1 ) |
|---|---|---|
| 3 | Lithium | 1.3158 |
| 4 | Beryllium | 2.6316 |
| 5 | Boron | 4.4379 |
| 6 | Carbon | 6.7114 |
| 7 | Nitrogen | 9.4937 |
| 8 | Oxygen | 12.701 |
| 9 | Fluorine | 16.376 |
| 10 | Neon | 20.534 |
| 11 | Sodium | 25.189 |
| 12 | Magnesium | 30.334 |
| 13 | Aluminum | 35.971 |
| 14 | Silicon | 42.008 |
| 15 | Phosphorous | 48.701 |
| 16 | Sulfur | 55.814 |
| 17 | Chlorine | 63.416 |
| 18 | Argon | 71.518 |
| 19 | Potassium | 80.118 |
| 20 | Calcium | 89.242 |
| 21 | Scandium | 98.873 |
| 22 | Titanium | 109.01 |
| 23 | Vanadium | 119.65 |
| 24 | Chromium | 130.80 |
| 25 | Manganese | 142.47 |
| 26 | Iron | 154.65 |
| 27 | Cobalt | 167.33 |
| 28 | Nickel | 180.53 |
| 29 | Copper | 194.25 |
| 30 | Zinc | 208.48 |
| 31 | Gallium | 223.21 |
| 32 | Germanium | 238.47 |
We have also added something interesting in [link] , the “atomic number.” This number is just the ranking of the elements in order of increasing mass. The atomic number then is just another name we have given to each element with no more significance than the names we have given. (Note again that Argon is placed before Potassium. There are other reasons for this, but this also makes sense in the data, since this way, the frequencies of the x-rays increase.)
Other than the fact that the x-ray frequencies consistently increase, there doesn’t seem to be any other obvious pattern in the data. We could look for a pattern by plotting the x-ray frequency versus the masses of the atoms, but this doesn’t show anything additional. Surprisingly, though, if we plot the x-ray frequency versus the atomic number, a clear pattern emerges, as we see in [link] .
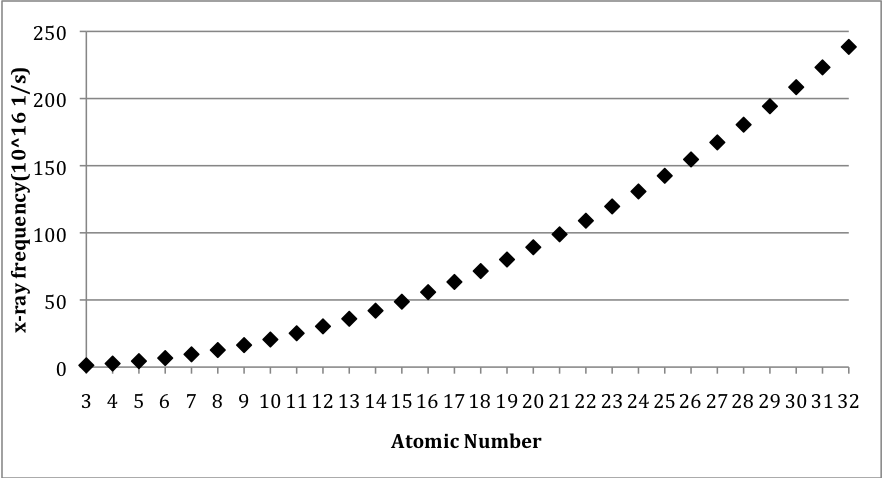
The frequencies don’t just increase with atomic number, they increase with a very smooth function. This type of graph might look familiar to you. It looks similar to a graph of y = x 2 , called a parabola. Is the graph in [link] a parabola? To find out, we need to know whether the x-ray frequency is a function of the atomic number squared. One way to do this is to plot the square root of the x-ray frequency versus the atomic number. This would be like plotting the square root of y versus x to see if y = x 2 . This new graph is shown in [link] .
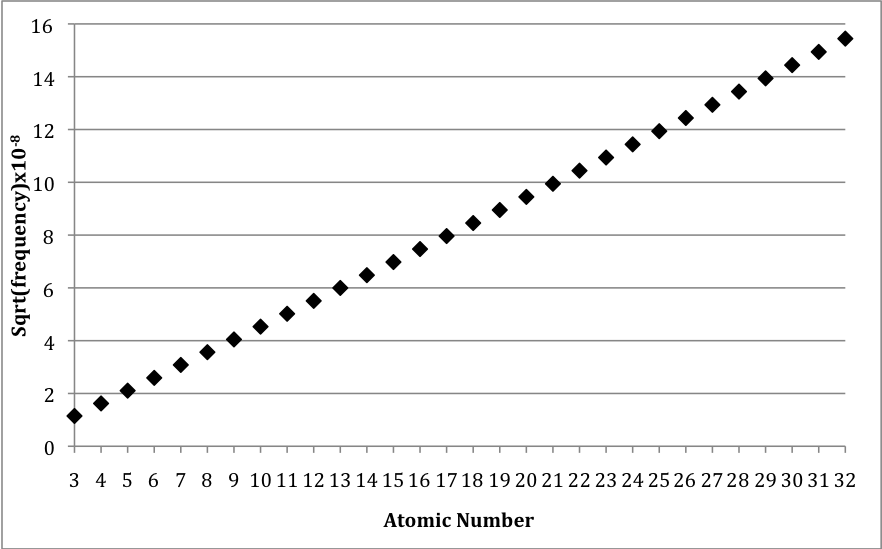
The graph in [link] is very significant. It shows that there is a simple relationship between the x-ray frequency emitted by each atom and the atomic number of the atom. But this is a strange result. The x-ray frequency is a physical property of each atom. The atomic number is just an integer that we assigned to each element based on its mass ranking. This is a surprise! Why would a physical property match up so strongly with a non-physical property like an integer in the mass rankings? There is only one possibility: the atomic number must also be a physical property of the atom. It is not an arbitrary number, even though we assigned it that way initially. It is a property of the atom.
The atomic number is also a special property of the atom because it is an integer, and integers are used to count objects or particles. This means that the atomic number must be counting some integer number of objects or particles in each atom, and that number must be unique for each atom. But we know that there is an integer that describes each atom: the number of protons and electrons that each atom has.
Our conclusion is therefore that the atomic number is a property of each atom which is equal to the number of protons in each atom and is also equal to the number of electrons in each atom. We have found a way to count the number of charges in each atom! There are two remarkable results to mention here. The first is that each atom has its own characteristic number of protons and electrons. This is not shared with any other atom. This suggests that these numbers must be important in determining the chemical and physical properties of the atom. The second is that every integer number of protons and electrons is accounted for. There are no gaps or breaks in [link] or in [link] or [link] . We have them all. There are no missing elements in the range from 3 to 32, nor for that matter from 1 to 114. This is why there are only a small number of elements (about 90 naturally occurring ones).
We now know what is unique about the atoms of different elements. It does make sense that atoms with different numbers of charged particles would interact differently, forming compounds with different chemical and physical properties. But we might imagine that atoms with similar (but not equal) numbers of charged particles would have fairly similar chemical and physical properties. As we will explore in much more detail later, this is not at all the case. In fact, it is possible to compare two elements with very similar atomic numbers, say Neon and Sodium, and find that their chemical properties are completely different. Neon is a gas, even at extremely low temperatures, and is so unreactive that it does not form compounds with any other elements. Sodium is a solid which is so reactive that its reactions with other elements are often violent and energetic. It seems clear that just knowing how many electrons an atom has is not sufficient to make predictions about how that atom might behave. We will need to refine our model with further observations.
By John S. Hutchinson, Rice University, 2011

Notification Switch
Would you like to follow the 'Concept development studies in chemistry 2012' conversation and receive update notifications?