Се дефинира векторски производ на два вектора и неговите својства.
Cross product and properties
Векторски производ на два вектора
За решавање на проблеми во кои се бара да се определи вектор кој ќе биде нормален на два дадени вектора, се дефинира друг вид на производ кој е векторска величина и се нарекува векторски производ и дефинира со:
Дефиницијa
.
Векторски
производ на векторите
и
е вектор
кој се означува со
и е определен со:
-
должина |
| = |
||
| sin
(
,
) ;
-
правец кој е нормален на рамнината во која лежат векторите
и
, односно
⊥
и
⊥
;
-
насоката на
е таква што векторите
,
и
образуваат десна тројка вектори, односно се однесуваат по правилото на десен винт (Сл. 1.8.).
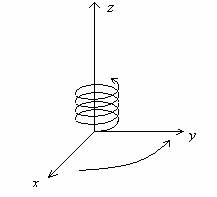 |
| Слика 1.8. Правило на десен винт |
Својства на векторскиот производ
Од дефиницијата за векторски производ следуваат следните негови својства:
1.
=
(антикомутативен закон)
2.
(дистрибутивен закон)
3.
λ(
) = (λ
)
×
=
× (λ
) (множење со скалар λ)
4. Ако
и
тогаш,
⇔
и
се колинеарни вектори (
||
).
5. Векторскиот производ меѓу единичните вектори е:
,
,
,
,
,
.
Ако векторите
и
се зададени со своите координати
= {
x
1
, y
1
, z
1 } и
= {
x
2
, y
2
, z
2 },
нивниот векторски производ изразен преку координати е
=
,
односно
,
или изразен преку троредна детерминанта
=
.
6. Плоштината на паралелограмот образуван од векторите
и
е еднаква со интензитетот на нивниот векторски производ
P
паралеограм = |
|,
бидејќи висината на паралелограмот е
h = |
| sin
(
,
), (Сл. 1.9) .
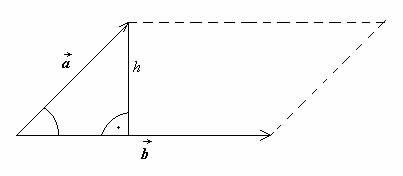 |
| Слика 1.9. Висина во паралелограм |
7. Плоштината P на триаголникот чии темиња се во три точки со зададени координати
A (
x
1
, y
1
, z
1 ),
B (
x
2
, y
2
, z
2 ) и
C (
x
3
, y
3
, z
3 ) е
P =
.
Забелешка : Двата вектора кои го образуваат паралелограмот (триаголникот) треба да имаат почеток во иста точка.
Пример 1. Ако
= {2, -1, 3},
= {0, 1, 7} и
= {1, 4, 5}, да се најде
?
Решение.
Најпрво се определуваат координатите на векторите
и
.
=
= {-23, 7, -1},
=
.
Бараниот производ е вектор чии координати се пресметуваат со детерминантата
=
= 2(
◄
Пример 2. Во триаголник со темиња
A (1, -1, 2),
B (5, -6, 2),
C (1, 3, -1) да се пресмета должината на висината
h спуштена од темето
B кон страната
AC .
Решение.
Плоштината на триаголникот
ABC ќе се пресмета со формулата
,
но и преку векторскиот производ (особина 7)
P =
,
од каде следува дека
.
Ги пресметуваме координатите на векторите кои се страни во триаголникот и имаат заеднички почеток во темето
A :
= {5 - 1, -6 - (-1), 2 - 2} = {4, -5, 0},
= {1 - 1, 3 -(-1), -1 - 2} = {0, 4, -3}.
Векторскиот производ е
=
= 15
+ 16
+ 12
= {15, 12, 16}
и има интензитет
Заменувајќи ги вредностите во изразот за пресметување на висината се добива
◄


