0.3 Gravity and mechanical energy  (Page 7/9)

Conservation of mechanical energy

The Law of Conservation of Energy states:

Energy cannot be created or destroyed, but is merely changed from one form into another.

Conservation of Energy

The Law of Conservation of Energy: Energy cannot be created or destroyed, but is merely changed from one form into another.

So far we have looked at two types of energy: gravitational potential energy and kinetic energy. The sum of the gravitational potential energy and kinetic energy is called the mechanical energy. In a closed system, one where there are no external forces acting, the mechanical energy will remain constant. In other words, it will not change (become more or less). This is called the Law of Conservation of Mechanical Energy and it states:

The total amount of mechanical energy in a closed system remains constant.

Conservation of Mechanical Energy

Law of Conservation of Mechanical Energy: The total amount of mechanical energy in a closed system remains constant.

This means that potential energy can become kinetic energy, or vise versa, but energy cannot 'dissappear'. The mechanical energy of an object moving in the Earth's gravitational field (or accelerating as a result of gravity) is constant or conserved, unless external forces, like air resistance, acts on the object.

We can now use the conservation of mechanical energy to calculate the velocity of a body in freefall and show that the velocity is independent of mass.

Show by using the law of conservation of energy that the velocity of a body in free fall is independent of its mass.

In general, mechanical energy is conserved in the absence of external forces. Examples of external forces are: applied forces, frictional forces and air resistance.

In the presence of internal forces like the force due to gravity or the force in a spring, mechanical energy is conserved.

The following simulation covers the law of conservation of energy.
run demo

Using the law of conservation of energy

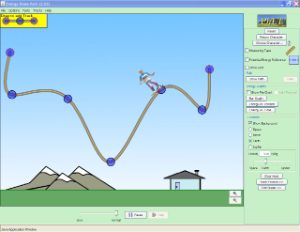
Mechanical energy is conserved (in the absence of friction). Therefore we can say that the sum of the $PE$ and the $KE$ anywhere during the motion must be equal to the sum of the $PE$ and the $KE$ anywhere else in the motion.

We can now apply this to the example of the suitcase on the cupboard. Consider the mechanical energy of the suitcase at the top and at the bottom. We can say:

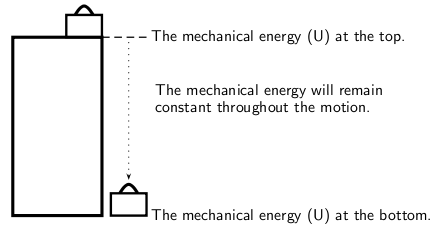
The suitcase will strike the ground with a velocity of $\mathrm{6,26}m·s{}^{-1}$ .