1. Home
  2. Maths test
  3. Maths test
  4. Force, momentum and impulse

0.2 Force, momentum and impulse  (Page 31/35)

<< Chapter < Page
  Maths test     Page 31 / 35
Chapter >> Page >
The force exerted on a spanner helps to loosen the bolt.

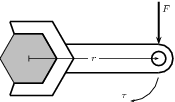
For example in [link] , if a force F of 10 N is applied perpendicularly to the spanner at a distance r of 0,3 m from the center of the bolt, then the torque applied to the bolt is:

τ = F ⊥ · r = ( 10 N ) ( 0 , 3 m ) = 3 N · m

If the force of 10 N is now applied at a distance of 0,15 m from the centre of the bolt, then the torque is:

τ = F ⊥ · r = ( 10 N ) ( 0 , 15 m ) = 1 , 5 N · m

This shows that there is less torque when the force is applied closer to the bolt than further away.

Loosening a bolt

If you are trying to loosen (or tighten) a bolt, apply the force on the spanner further away from the bolt, as this results in a greater torque to the bolt making it easier to loosen.

Any component of a force exerted parallel to an object will not cause the object to turn. Only perpendicular components cause turning.
Torques

The direction of a torque is either clockwise or anticlockwise. When torques are added, choose one direction as positive and the opposite direction as negative. If equal clockwise and anticlockwise torques are applied to an object, they will cancel out and there will be no net turning effect.

Several children are playing in the park. One child pushes the merry-go-round with a force of 50 N. The diameter of the merry-go-round is 3,0 m. What torque does the child apply if the force is applied perpendicularly at point A?

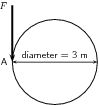
  1. The following has been given:

    • the force applied, F  = 50 N
    • the diameter of the merry-go-round, 2 r  = 3 m, therefore r  = 1,5 m.

    The quantities are in SI units.

  2. We are required to determine the torque applied to the merry-go-round. We can do this by using:

    τ = F ⊥ · r

    We are given F ⊥ and we are given the diameter of the merry-go-round. Therefore, r = 1,5 m.

  3. τ = F ⊥ · r = ( 50 N ) ( 1 , 5 m ) = 75 N · m

  4. 75  N · m of torque is applied to the merry-go-round.

Kevin is helping his dad replace the flat tyre on the car. Kevin has been asked to undo all the wheel nuts. Kevin holds the spanner at the same distance for all nuts, but applies the force at two angles (90 ∘ and 60 ∘ ). If Kevin applies a force of 60 N, at a distance of 0,3 m away from the nut, which angle is the best to use? Prove your answer by means of calculations.

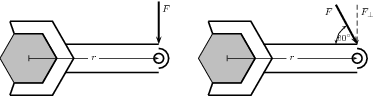
  1. The following has been given:

    • the force applied, F  = 60 N
    • the angles at which the force is applied, θ = 90 ∘ and θ = 60 ∘
    • the distance from the centre of the nut at which the force is applied, r  = 0,3 m

    The quantities are in SI units.

  2. We are required to determine which angle is more better to use. This means that we must find which angle gives the higher torque. We can use

    τ = F ⊥ · r

    to determine the torque. We are given F for each situation. F ⊥ = F sin θ and we are given θ . We are also given the distance away from the nut, at which the force is applied.

  3. F ⊥ = F

    τ = F ⊥ · r = ( 60 N ) ( 0 , 3 m ) = 18 N · m
  4. τ = F ⊥ · r = F sin θ · r = ( 60 N ) sin ( θ ) ( 0 , 3 m ) = 15 , 6 N · m

  5. The torque from the perpendicular force is greater than the torque from the force applied at 60 ∘ . Therefore, the best angle is 90 ∘ .
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Maths test. OpenStax CNX. Feb 09, 2011 Download for free at http://cnx.org/content/col11236/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Maths test' conversation and receive update notifications?

Ask