| << Chapter < Page | Chapter >> Page > |
As described in Review of past work , a number is a way of representing quantity. The numbers that will be used in high school are all real numbers, but there are many different ways of writing any single real number.
This chapter describes rational numbers .
Khan academy video on integers and rational numbers
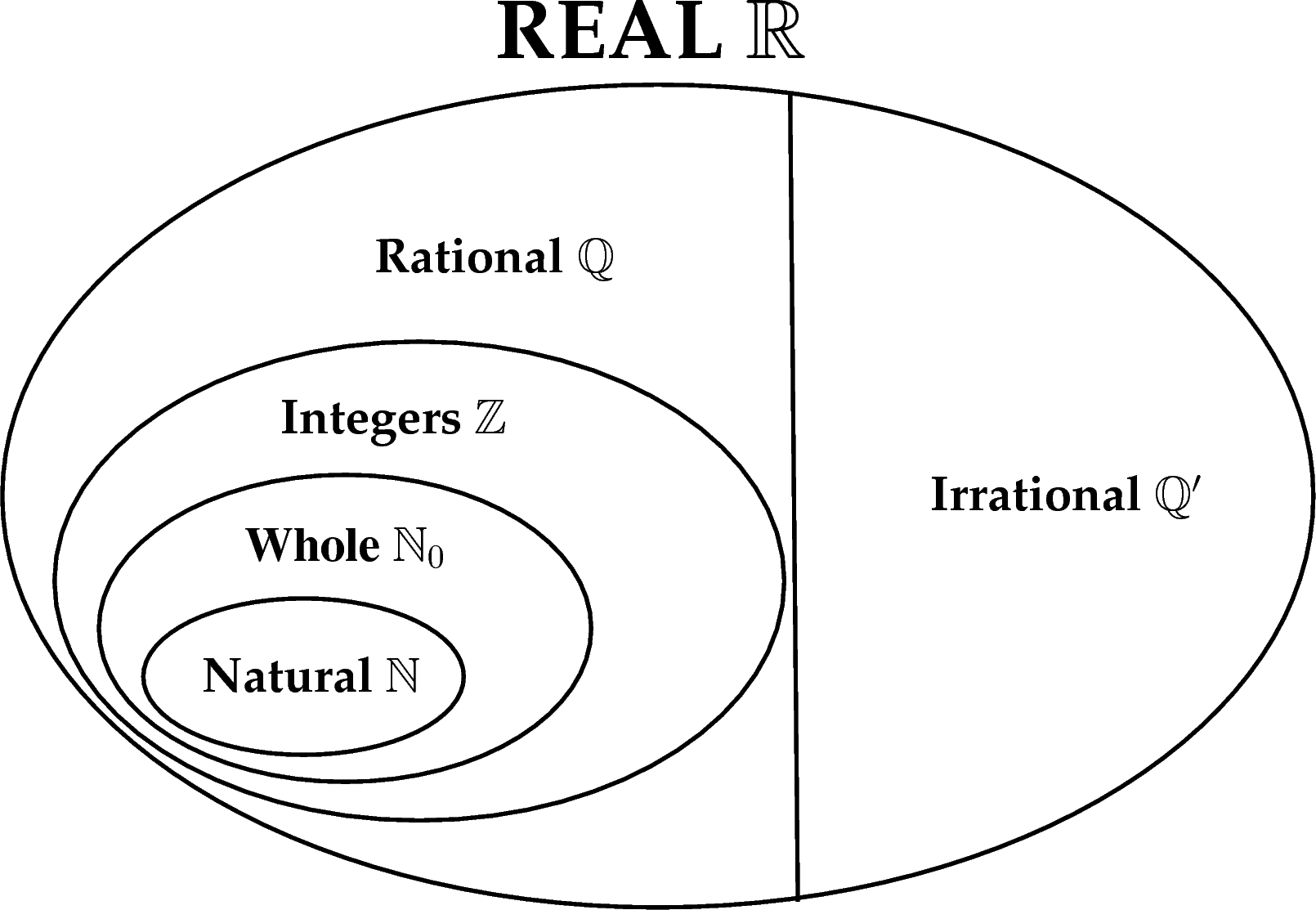
The term whole number does not have a consistent definition. Various authors use it in many different ways. We use the following definitions:
The following numbers are all rational numbers.
You can see that all denominators and all numerators are integers.
A rational number is any number which can be written as:
where and are integers and .
Note that because we can write as (in other words, one can always find an equivalent rational expression where ) mathematicians typically define rational numbers not as both and being integers, but rather that is an integer and is a natural number. This avoids having to worry about zero in the denominator.
This means that all integers are rational numbers, because they can be written with a denominator of 1.
Therefore
are not examples of rational numbers, because in each case, either the numerator or the denominator is not an integer.
A number may not be written as an integer divided by another integer, but may still be a rational number. This is because the results may be expressedas an integer divided by an integer. The rule is, if a number can be written as a fraction of integers, it is rational even if it can also be written in anotherway as well. Here are two examples that might not look like rational numbers at first glance but are because there are equivalent forms that are expressed as aninteger divided by another integer:
All integers and fractions with integer numerators and denominators are rational numbers. There are two more forms of rational numbers.
You can write the rational number as the decimal number 0,5. Write the following numbers as decimals:
Do the numbers after the decimal comma end or do they continue? If they continue, is there a repeating pattern to the numbers?
You can write a rational number as a decimal number. Two types of decimal numbers can be written as rational numbers:

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?