| << Chapter < Page | Chapter >> Page > |
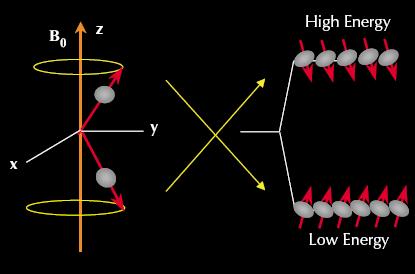
Considering the case of a proton under the influence of an external magnetic field, it will be in one of two possible energy states depending on the orientation of the precession axis. If the axis is parallel to B o , the proton is in the lower energy state (preferred state) and in the higher energy state if anti-parallel shown by [link] .
We define the net magnetization per unit volume of material, M o , from Curie’s law as [link] , where N = number of protons, h = Planck's constant (6.626 x 10 -34 Js), I = spin quantum number of the nucleus, k = Boltzmann's constant (1.381 x 10 -23 m 2 Kg s -2 K -1 ), and T = temperature (K)
The protons are said to be polarized completely once they are all aligned with the static external field. Polarization grows with a time constant called the longitudinal relaxation time (T 1 ) as shown in [link] , where t = time of exposure to B o , M z (t) = magnitude of magnetization at time t, with B o along z-axis and T 1 = time at which M z (t) reaches 90% of its final value, i.e., M o .
T 1 is the time at which M z (t) reaches 63% of its final value, M o . A typical T 1 relaxation experiment involves application of a 90 o RF pulse that rotates the magnetization to the transverse direction. With time, the magnetization returns to its original value in the same fashion described by the above equation.
Click on the video below to see the mechanism of T 1 relaxation
T
1 relaxation mechanism.
Once the polarization is complete, the magnetization direction is tipped from the longitudinal plane to a transverse plane by applying an oscillating field B 1 perpendicular to B o . The frequency of B 1 must equal the Larmor frequency of the material from B o . This oscillating field causes a possible change in energy state, and in-phase precession. The total phenomenon is called nuclear magnetic resonance as shown in [link] .
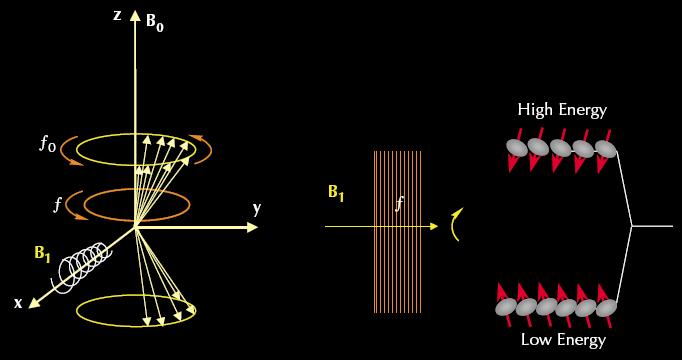
The oscillating field is generally pulsed in nature and so terms in books such a 180 o pulse or 90 o pulse indicates the angle through which the net magnetization gets tipped over. Application of a 90 o pulse causes precession in the transverse phase. When the field B 1 is removed, the nuclei begin to de-phase and the net magnetization decreases. Here a receiver coil detects the decaying signal in a process called free induction decay (FID) . This exponential decay has an FID time constant (T 2 ) which is in the order of microseconds.
The time constant of the transverse relaxation is referred as T 2 , and the amplitude of the decaying signal is given by [link] , with symbols as defined earlier.
Click on the video below to see the mechanism of T 2 relaxation
T
2 relaxation mechanism.
The de-phasing caused by T 1 relaxation can be reversed by applying a 180 o pulse after a time τ has passed after application of the initial 90 o pulse. Thus the phase of the transverse magnetization vector is now reversed by 180 o so that “slower” vectors are now ahead of the “faster” vectors. These faster vectors eventually over-take the slower vectors and cause rephasing which is detected by a receiver coil as a s pin echo . Thus time τ also passes between the application of the 180 o pulse and the maximum peak in the spin echo. The entire sequence is illustrated in [link] . A single echo decays very quickly and hence a series of 180 0 pulses are applied repeatedly in a sequence called the Carr-Purcell-Meiboom-Gill (CPMG) sequence .

Notification Switch
Would you like to follow the 'Nanomaterials and nanotechnology' conversation and receive update notifications?