| << Chapter < Page | Chapter >> Page > |
The answer, rounded, is the same.
In many fields, especially in the sciences, it is common to multiply decimals by powers of 10. Let’s see what happens when we multiply 1.9436 by some powers of 10.
The number of places that the decimal point moves is the same as the number of zeros in the power of ten. [link] summarizes the results.
| Multiply by | Zeros | Decimal point moves . . . |
|---|---|---|
| 10 | 1 | 1 place to the right |
| 100 | 2 | 2 places to the right |
| 1,000 | 3 | 3 places to the right |
| 10,000 | 4 | 4 places to the right |
We can use this pattern as a shortcut to multiply by powers of ten instead of multiplying using the vertical format. We can count the zeros in the power of 10 and then move the decimal point that same number of places to the right.
So, for example, to multiply 45.86 by 100, move the decimal point 2 places to the right.
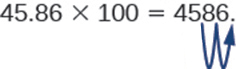
Sometimes when we need to move the decimal point, there are not enough decimal places. In that case, we use zeros as placeholders. For example, let’s multiply 2.4 by 100. We need to move the decimal point 2 places to the right. Since there is only one digit to the right of the decimal point, we must write a 0 in the hundredths place.
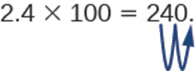
When dividing by powers of 10, simply take the opposite approach and move the decimal to the left by the number of zeros in the power of ten.
Let’s see what happens when we divide 1.9436 by some powers of 10.
If there are insufficient digits to move the decimal, add zeroes to create places.
Scientific notation is used to express very large and very small numbers as a product of two numbers. The first number of the product, the digit term, is usually a number not less than 1 and not greater than 10. The second number of the product, the exponential term, is written as 10 with an exponent. Some examples of scientific notation are given in [link] .
| Standard Notation | Scientific Notation |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 −1 |
| 0.01 | 1 × 10 −2 |
Scientific notation is particularly useful notation for very large and very small numbers, such as 1,230,000,000 = 1.23 × 10 9 , and 0.00000000036 = 3.6 × 10 −10 .
Converting any number to scientific notation is straightforward. Count the number of places needed to move the decimal next to the left-most non-zero digit: that is, to make the number between 1 and 10. Then multiply that number by 10 raised to the number of places you moved the decimal. The exponent is positive if you moved the decimal to the left and negative if you moved the decimal to the right. So
and
The power (exponent) of 10 is equal to the number of places the decimal is shifted.
The common logarithm (log) of a number is the power to which 10 must be raised to equal that number. For example, the common logarithm of 100 is 2, because 10 must be raised to the second power to equal 100. Additional examples are in [link] .

Notification Switch
Would you like to follow the 'Microbiology' conversation and receive update notifications?