| << Chapter < Page | Chapter >> Page > |
Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x -intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x -intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.
If a rational function has x -intercepts at vertical asymptotes at and no then the function can be written in the form:
where the powers or on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor can be determined given a value of the function other than the x -intercept or by the horizontal asymptote if it is nonzero.
Given a graph of a rational function, write the function.
Write an equation for the rational function shown in [link] .
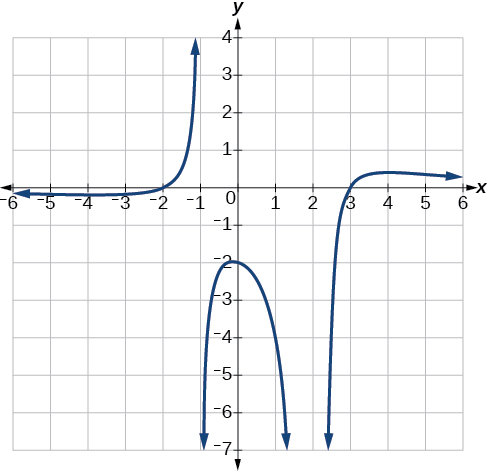
The graph appears to have x -intercepts at and At both, the graph passes through the intercept, suggesting linear factors. The graph has two vertical asymptotes. The one at seems to exhibit the basic behavior similar to with the graph heading toward positive infinity on one side and heading toward negative infinity on the other. The asymptote at is exhibiting a behavior similar to with the graph heading toward negative infinity on both sides of the asymptote. See [link] .
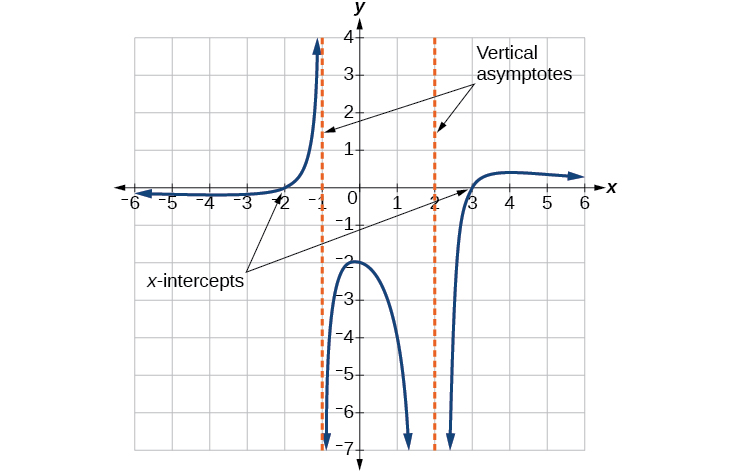
We can use this information to write a function of the form
To find the stretch factor, we can use another clear point on the graph, such as the y -intercept
This gives us a final function of
Access these online resources for additional instruction and practice with rational functions.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?