Probability: part 1

Outcome

An outcome of an experiment is a single result of that experiment.

• A possible outcome of Experiment 1: the value on the top face is '3'
• A possible outcome of Experiment 2: the total value on the top faces is '9'

Sample space

The sample space of an experiment is the complete set of possible outcomes of the experiment.

• Experiment 1: the sample space is 1,2,3,4,5,6
• Experiment 2: the sample space is 2,3,4,5,6,7,8,9,10,11,12

Event

An event is any set of outcomes of an experiment.

• A possible event of Experiment 1: an even number being on the top face of the die
• A possible event of Experiment 2: the numbers on the top face of each die being equal

Random experiments

The term random experiment or statistical experiment is used to describe any repeatable process, the results of which are analyzed in some way. For example, flipping a coin and noting whetheror not it lands heads-up is a random experiment because the process is repeatable. On the other hand, your reading this sentence for the first time andnoting whether you understand it is not a random experiment because it is not repeatable (though making a number of random people read it and noting whichones understand it would turn it into a random experiment).

Venn diagrams

A Venn diagram can be used to show the relationship between the possible outcomes of a random experiment and thesample space. The Venn diagram in [link] shows the difference between the universal set, a sample space and events and outcomes as subsets ofthe sample space.

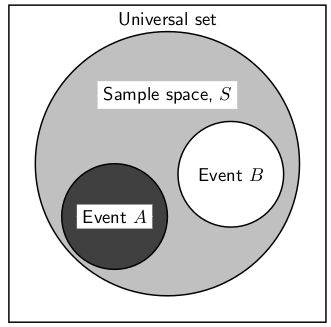
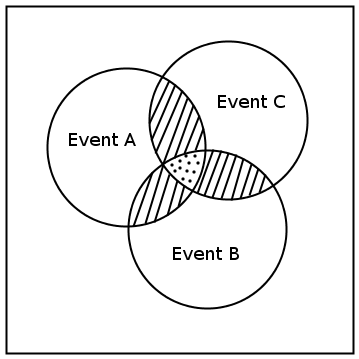
We can draw Venn diagrams for experiments with two and three events. These are shown in [link] and [link] . Venn diagrams for experiments with more than three events are more complex and are not covered at this level.

Interesting fact

The Greek, Russian and Latin alphabets can be illustrated using Venn diagrams. All these alphabets have some common letters. The Venn diagram is given below:

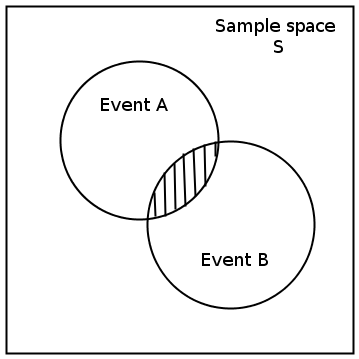
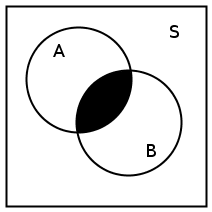
The union of $A$ and $B$ is the set of all elements in $A$ or in $B$ (or in both). $A\mathbf{or}B$ is also written $A\cup B$ . The intersection of $A$ and $B$ is the set of all elements in both $A$ and $B$ . $A\mathbf{and}B$ is also written as $A\cap B$ .

Venn diagrams can also be used to indicate the union and intersection between events in a sample space ( [link] and [link] ).