| << Chapter < Page | Chapter >> Page > |
To do so, we outline an approach by Elias [link] . Let be a natural number, and let be the binary form for . For example, , and so on. Another challenge is that the length of this representation, , is unknown. Let , for example . We can now define . For example, for n=5, we have . Therefore, and . We note in passing that the first 2 bits of describe the length of , which is 2, the middle 2 bits describe , which is 3, and the last 3 bits describe , giving the actual number 5. It is easily seen that
Having described an efficient way to encode an index, in particular a large one, we can employ this technique in sliding window codingas developed by Wyner and Ziv [link] .
Take a fixed window of length and a source that generates characters. Define the history as , this is the portion of the data that we have already processed and thus know.Our goal is to encode the phrase , where is not fixed. The length is chosen such that there exists
for some . For example, if and we have processed the first 5 symbols , then and , where is the history and we begin encoding after that part.
The actual encoding of the phrase sends bits, where
First we encode ; then either the index into history is encoded or is encoded uncompressed; finally, the first characters are removed from the history database, and is appended to its end. The latter process gives this algorithm a sliding window flavor.
This rather simple algorithm turns out to be asymptotically optimal in the limit of large . That is, it achieves the entropy rate.To see this, let us compute the compression factor. Consider where , , , and , where is the number of phrases required to encode . The number of bits needed to encoded using the sliding window algorithm is
Therefore, the compression factor satisfies
Claim 3 [link] As and , the compression factor converges to the entropy rate .
A direct proof is complicated, because the location of phrases is a random variable, making a detailed analysis complicated. Let us try to simplify the problem.
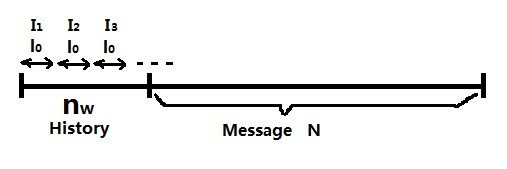
Take that divides to create intervals, where , which is related to the window size in the algorithm from [link] . This partition into blocks appears in [link] . Denote by the smallest value for which . Using Kac's lemma [link] ,
Claim 4 [link] We have the following convergence as increases,

Notification Switch
Would you like to follow the 'Universal algorithms in signal processing and communications' conversation and receive update notifications?