2.4 Similarity

Mathematics

Grade 9

Algebra and geometry

Module 10

Similarity

ACTIVITY 1:

To practically investigate the conditions for similarity

1. The pentagons ABDEF and LCMRK are given (A-6). LCMRK is an enlargement of ABDEF. What is the scale factor by which ABDEF were enlarged to give LCMRK?

2. Write down the ratios between the corresponding pairs of sides of ABDEF and LCMRK.

3. Write down the relationship between the corresponding pairs of angles of the two figures.

4. These two figures are not congruent. What do we call them?

5. Name as many as possible e x amples of this phenomenon in real life.

Similar figures:

• The pentagons in the activity above are similar. They have the same form, but do not have the same size.
• Their corresponding angles have the same magnitudes.
• Their corresponding sides are in the same ratio.

Therefore $\frac{\text{LK}}{\text{AF}}=\frac{\text{KR}}{\text{FE}}=\frac{\text{MR}}{\text{DE}}=\frac{\text{CM}}{\text{BD}}=\frac{\text{CL}}{\text{BA}}=\frac{3}{1}$ This constant ratio also is the scale factor of the enlargement.

• We say that ABDEF  LCMRK. Note that the order of the letters is in the same order of the angles which are equal and the sides which are in proportion. (The symbol for similarity is )

Homework assignment

1. Measure the lengths of the sides and the magnitudes of the angles in the following figures (A-7) and decide whether they are similar or not. If the two figures are not similar, give a reason why they are not similar.

2. If the corresponding a ngles of two quadrilaterals are equ a l , are they necess a rily also simil a r ?

3. If corresponding sides of two quadrilaterals are proportion a l , are they necess a rily also simil a r ?

• In the homework assignment above you saw that, for quadrilaterals to be similar, both conditions of similarity must be satisfied. In other words, the corresponding angles must be equal and the corresponding sides must be proportional. Do the same conditions also apply to triangles?

ACTIVITY 2:

To practically investigate the conditions for similarity in triangles

[LO 3.5]

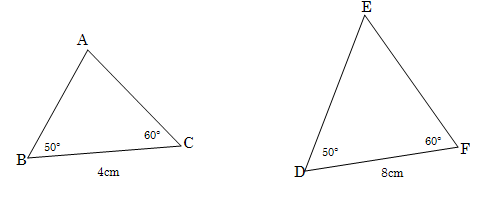
Construct ΔABC and ΔDEF. Calculate the magnitudes A and E.

1.2 Are the corresponding angles of the two triangles equal?

1.3 Complete the following:

$\frac{\text{AB}}{\text{ED}}=$ ....................

$\frac{\text{BC}}{\text{DF}}=$ ....................

$\frac{\text{AC}}{\text{EF}}=$ ....................

1.4 Are the corresponding sides of the two triangles proportional?

1.5 Are the two triangles similar?

1.6 Complete the following: If the corresponding angles of two triangles are equal, their corresponding sides are necessarily also always ......................... This means that, if the corresponding angles of triangles are equal the triangles are .........................

2.1 Construct the following two triangles:

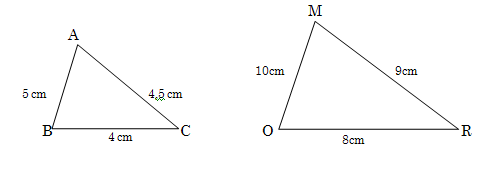
2.2 Are the sides of the two triangles proportional?

2.3 Measure all the angles of ΔABC and ΔMOR. What do you find?

2.4 Is ΔABC  ΔMOR?

2.5 Complete the following: If the corresponding sides of two triangles are proportional then their corresponding ..................................... are equal. That therefore means that, if the corresponding sides of two triangles are proportional, the triangles are.....................................

• We therefore see that with triangles only one of the conditions of similarity have to be present for triangles to be similar.
• That means that, if the three a ngles of one tri a ngle are equal to the three a ngles of the other tri a ngle , then the corresponding sides of the two triangles are proportional and the triangles are therefore also similar.
• It also means that, if the corresponding sides of the triangles are proportion a l , then the corresponding angles of the two triangles are equal and the triangles are therefore also similar.