4.2 Proper fractions, improper fractions, and mixed numbers

Section overview

• Positive Proper Fractions
• Positive Improper Fractions
• Positive Mixed Numbers
• Relating Positive Improper Fractions and Positive Mixed Numbers
• Converting an Improper Fraction to a Mixed Number
• Converting a Mixed Number to an Improper Fraction

Now that we know what positive fractions are, we consider three types of positive fractions: proper fractions, improper fractions, and mixed numbers.

Positive proper fractions

Positive proper fraction

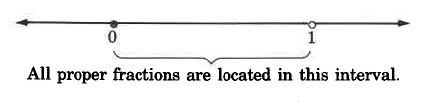
The closed circle at 0 indicates that 0 is included, while the open circle at 1 indicates that 1 is not included.

Some examples of positive proper fractions are

$$ $\frac{1}{2}$ , $\frac{3}{5}$ , $\frac{\text{20}}{\text{27}}$ , and $\frac{\text{106}}{\text{255}}$

Note that , , , and .

Positive improper fractions

Positive improper fractions

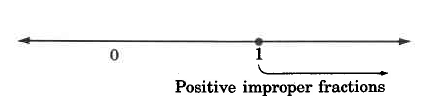
Some examples of positive improper fractions are

$\frac{3}{2}$ , $\frac{8}{5}$ , $\frac{4}{4}$ , and $\frac{\text{105}}{\text{16}}$

Note that $3\ge 2$ , $8\ge 5$ , $4\ge 4$ , and $\text{105}\ge \text{16}$ .

Positive mixed numbers

Positive mixed numbers

$\text{nonzero whole number}+\text{proper fraction}$

is called a positive mixed number . For example, $2\frac{3}{5}$ is a mixed number. On the number line, mixed numbers are located in the interval to the right of (and includ­ing) 1. Mixed numbers are always greater than or equal to 1.

Relating positive improper fractions and positive mixed numbers

A relationship between improper fractions and mixed numbers is suggested by two facts. The first is that improper fractions and mixed numbers are located in the same interval on the number line. The second fact, that mixed numbers are the sum of a natural number and a fraction, can be seen by making the following observa­tions.

Divide a whole quantity into 3 equal parts.

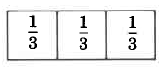
Now, consider the following examples by observing the respective shaded areas.

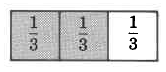
In the shaded region, there are 2 one thirds, or $\frac{2}{3}$ .

$2\left(\frac{1}{3}\right)=\frac{2}{3}$

There are 3 one thirds, or $\frac{3}{3}$ , or 1.

$3\left(\frac{1}{3}\right)=\frac{3}{3}\text{or}1$

Thus,

$\frac{3}{3}=1$

Improper fraction = whole number.

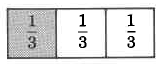
There are 4 one thirds, or $\frac{4}{3}$ , or 1 and $\frac{1}{3}$ .

$4\left(\frac{1}{3}\right)=\frac{4}{3}$ or $1\text{and}\frac{1}{3}$

The terms 1 and $\frac{1}{3}$ can be represented as $1+\frac{1}{3}$ or $1\frac{1}{3}$

Thus,

$\frac{4}{3}=1\frac{1}{3}$ .

Improper fraction = mixed number.

There are 5 one thirds, or $\frac{5}{3}$ , or 1 and $\frac{2}{3}$ .

$5\left(\frac{1}{3}\right)=\frac{5}{3}\text{or}1\text{and}\frac{2}{3}$