| << Chapter < Page | Chapter >> Page > |
For the following problems, simplify the expressions.
61
438
2
79
8
43
For the following problems, write the appropriate relation symbol in place of the .
For the following problems, state whether the letters or symbols are the same or different.
![]()
>and ≮
different
Represent the sum of and two different ways.
For the following problems, use algebraic notataion.
8 plus 9
62 divided by
8 times
6 times , minus 2
divided by
divided by , minus 12
zero minus times
Is every natural number a whole number?
yes
Is every rational number a real number?
For the following problems, locate the numbers on a number line by placing a point at their (approximate) position.
2
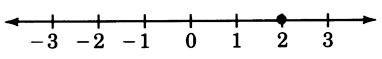
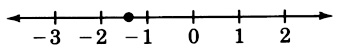
0
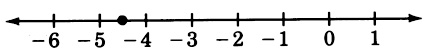
Draw a number line that extends from 10 to 20. Place a point at all odd integers.
Draw a number line that extends from to . Place a point at all negative odd integers and at all even positive integers.

Draw a number line that extends from to . Place a point at all integers that are greater then or equal to but strictly less than 5.
Draw a number line that extends from to . Place a point at all real numbers that are strictly greater than but less than or equal to 7.
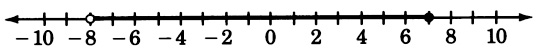
Draw a number line that extends from to . Place a point at all real numbers between and including and 4.
For the following problems, write the appropriate relation symbol
Is there a smallest two digit integer? If so, what is it?
Is there a smallest two digit real number? If so, what is it?
For the following problems, what integers can replace so that the statements are true?
The temperature today in Los Angeles was eighty-two degrees. Represent this temperature by real number.
The temperature today in Marbelhead was six degrees below zero. Represent this temperature by real number.
On the number line, how many units between and 2?
On the number line, how many units between and 0?
4
is an illustration of the
is an illustration of the __________ property of __________.
commutative, multiplication
Use the commutative properties of addition and multiplication to write equivalent expressions for the following problems.
Simplify the following problems using the commutative property of multiplication. You need not use the distributive property.
0
For the following problems, use the distributive property to expand the expressions.
For the following problems, write the expressions using exponential notation.
to the fifth.
cubed.
squared minus to the fourth.
cubed plus 2 times to the seventh.
For the following problems, expand the terms so that no exponents appear.
Choose values for and to show that
Choose value for to show that
(a) any value except zero
(b) only zero
Simplify the following problems.
366
10

Notification Switch
Would you like to follow the 'Basic mathematics review' conversation and receive update notifications?