3.1 Convolución de tiempo-continuo  (Page 2/2)

Proceso ii: el método largo

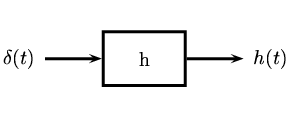
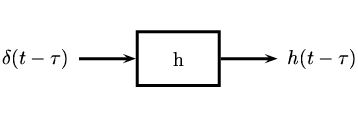
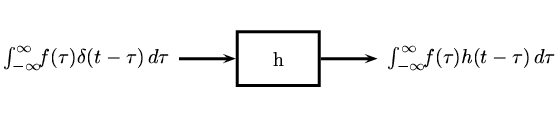
Este método realmente no es muy diferente del anterior, sin embargo es un poco mas riguroso y mas largo. Esperanzadamente si no se comprendió bien el método de arriba, esto te ayudara para terminar de entender la convolución.

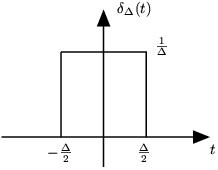
El primer paso en este método es definir una realización particular de la función de impulso unitario . Para esto usaremos ${\delta }_{\Delta }(t)=\begin{cases}\frac{1}{\Delta } & \text{if $-\left(\frac{\Delta }{2}\right)< t< \frac{\Delta }{2}$}\\ 0 & \text{otherwise}\end{cases}$

Después de definir la realización de la unidad de respuesta al impulso, podemos obtener nuestra integral de convolución de los siguientes pasos que se encuentran en la siguiente tabla. Notemos que la columna de la izquierda representa la entrada y la columna de la derecha es la salida del sistema dada esa entrada.

Implementación de la convolución

Tomando una visión mas cercana de la integral de convolución, encontramos que estamos multiplicando la señal de entrada por una respuesta al impulso invertida en tiempo e integrándola. Esto nos dará el valor de la salida de un valor dado de $t$ . Si después nosotros cambiamos la respuesta al impulso invertida en tiempo por una pequeña cantidad, obtenemos la salida para otro valor de $t$ . Repitiendo esto para cada posible valor de $t$ , nos da la función total de salida. Nosotros nunca haremos este método a mano, nos proporciona información con algunas entradas de que es lo que esta pasando. Encontramos que esencialmente estamos revirtiendo la función de la respuesta al impulso y desplazándola a través de la función de entrada, integrándola como vamos. Este método, descrito como el metodo gráfico , nos proporciona una manera sencilla de resolver las salidas para señales sencillas, mientras tanto mejoraremos nuestra intuición para los casos mas complejos donde confiaremos en las computadoras. De hecho las Texas Instruments se convierten en Procesamiento Digital de Señales las cuales tienen un conjunto especial para cómputos así como para la convolución.

Ejemplos básicos

Veamos ejemplos de la convolución básica de tiempo-continuo para poder expresar algunas ideas mencionadas anteriormente en el ejemplo corto. Vamos a convolver dos pulsos unitarios, $x(t)$ y $h(t)$ .

Reflejada y desplazada

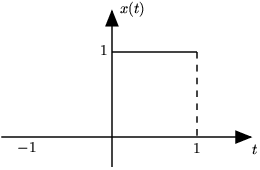
Ahora tomaremos una de las funciones y la reflejaremos a través del eje de las y. Después debemos desplazar la función, así como el origen, el punto de la función que originalmente estaba en el origen, esta marcada como el punto $\tau$ . Este paso se muestra en la siguiente figura, $h(t-\tau )$ . Como la convolución es conmutativa no importa que función es reflejada y desplazada, sin embargo conforme las funciones se vuelven mas complicadas reflejar y desplazar la “correcta” nos hará el problema mas sencillo.

Regiones de integración

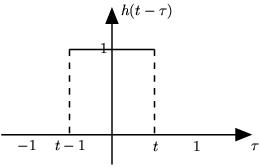
Ahora veremos la función y dividiremos su dominio en dos límites diferentes de integración. Estas dos regiones diferentes pueden ser entendidas pensando en como nos desplazamos $h(t-\tau )$ sobre la otra función. Si la función fuera mas complicada necesitaremos tener mas limites para que las partes sobrepuestas de las dos funciones puedan ser expresadas en una integral lineal sencilla. Para este problema tendremos las siguientes cuatro regiones. Compárense estos limites de integración con los de los bosquejos de $h(t-\tau )$ y $x(t)$ para ver si se puede entender el por que tenemos cuatro regiones. Nótese que $t$ en los limites de integración se refiere al lado derecho de la función $h(t-\tau )$ , marcada como $t$ entre cero y uno en la gráfica.

Los cuatro limites de integración

1. $t< 0$
2. $0\le t< 1$
3. $1\le t< 2$
4. $t\ge 2$

Usando la integral de convolución

Finalmente estamos listos para unas pequeñas matemáticas. Usando la integral de convolución, integremos el producto de $x(t)h(t-\tau )$ . Para la primer y cuarta región es trivial pues siempre será, $0$ . La segunda región, $0\le t< 1$ , requiere las siguientes matemáticas:

Resultados de la convolución

Así, obtenemos los siguientes resultados para nuestras cuatro regiones: