| << Chapter < Page | Chapter >> Page > |
Two 10 k resistors are connected in series. Calculate the equivalent resistance.
Since the resistors are in series we can use:
The equivalent resistance of two 10 k resistors connected in series is 20 k .
Two resistors are connected in series. The equivalent resistance is 100 . If one resistor is 10 , calculate the value of the second resistor.
Since the resistors are in series we can use:
We are given the value of and .
The second resistor has a resistance of 90 .
In contrast to the series case, when we add resistors in parallel, we create more paths along which current can flow. By doing this we decrease the total resistance of the circuit!
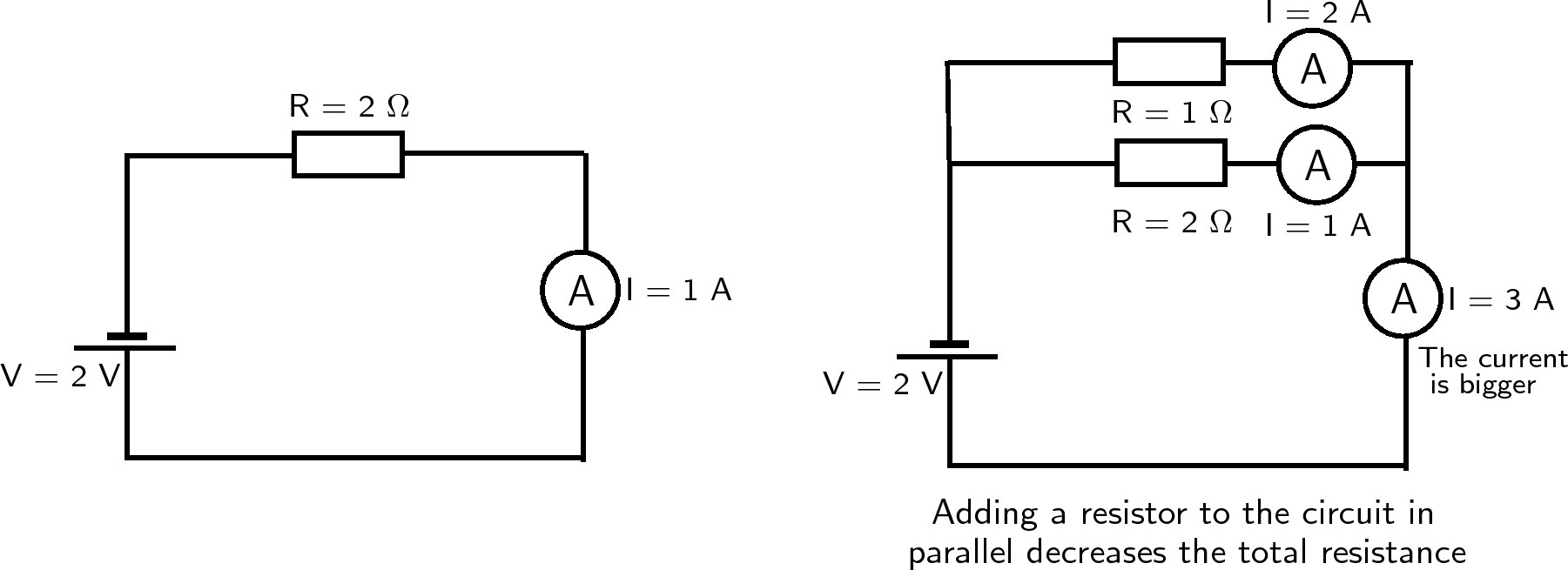
Take a look at the diagram below. On the left we have the same circuit as shown on the left in [link] with a battery and a resistor. The ammeter shows a current of 1 ampere. On the right we have added a second resistor in parallel to the first resistor. This has increased the number of paths (branches) the charge can take through the circuit - the total resistance has decreased. You can see that the current in the circuit has increased. Also notice that the current in the different branches can be different (in this case 1 A and 2 A) but must add up to the current through the battery (3 A). Since the total current in the circuit is equal to the sum of the currents in the parallel branches, a parallel circuit is sometimes called a current divider .
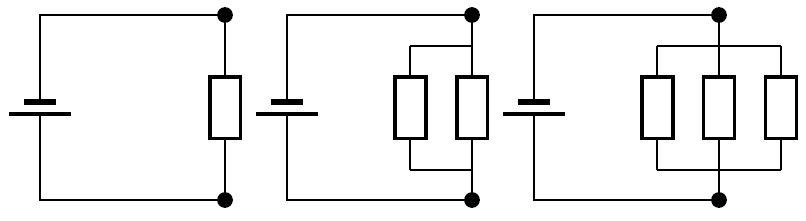
Look at the following circuit diagrams. The battery is the same in all cases. All that changes is that more resistors are added between the points marked by the black dots. If we were to measure the potential difference between the two dots in these circuits we would get the same answer for all three cases.
Let's look at two resistors in parallel more closely. When you construct a circuit you use wires and you might think that measuring the voltage in different places on the wires will make a difference. This is not true. The potential difference or voltage measurement will only be different if you measure a different set of components. All points on the wires that have no circuit components between them will give you the same measurements.
All three of the measurements shown in the picture below (i.e. A–B, C–D and E–F) will give you the same voltage. The different measurement points on the left (i.e. A, E, C) have no components between them so there is no change in potential energy. Exactly the same applies to the different points on the right (i.e. B, F, D). When you measure the potential difference between the points on the left and right you will get the same answer.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?