| << Chapter < Page | Chapter >> Page > |
Now, we interpret second condition according to which the whole logarithmic expression within the square root should be a non-negative number.
We use the fact that . This gives us the inequality as given here,
Clearly, “2” and “4” are the roots of the corresponding quadratic equation. Following sign scheme, we pick middle negative interval :
Domain of the function
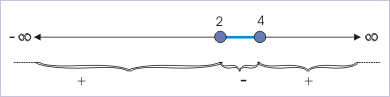
Now, the interval of “x” valid for real values of “f(x)” is the one which satisfies both conditions simultaneously i.e. the interval common to two intervals determined. Hence,
Domain of the function
Problem : Find the domain of the function given by :
Solution : The function is square root of an expression, consisting logarithmic functions. Here, we first need to simplify expression, using logarithmic identities, before attempting to find domain of the function. Let us first simplify the middle term of the given expression, using logarithmic identities :
We observe that all logarithmic functions have the base of “0.2”. Let us consider that , then logarithmic expression within square root is :
Now, this expression is non-negative for square root to be real. Hence,
But, we see that is a positive number as term is positive. It means that :
Note that we have reversed the inequality as the base is 0.2, which is less than 1. Further, we have substituted as :
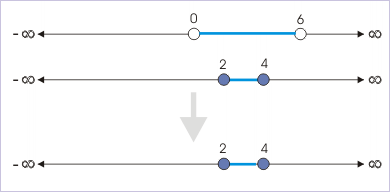
This logarithmic function is valid by definition for all positive value of “x”. Now, the domain of given function is the intersection of two intervals as shown in the figure.
Domain of the function
Problem : Find range of the function :
Solution : We observe that for x≤0,
For x>0
We can see that for all x. Hence,
Here, critical points are 0,1. Thus, range of the given function is :
Find the domain of the function given by :
The exponent of the exponential function is inverse trigonometric function. Exponential function is real for all real values of exponent. We see here that given function is real for the values of “x” corresponding to which arcsine function is real. Now, domain of arcsine function is [-1,1]. This is the interval of "x" for which arcsine is real. Hence, domain of the given function, “f(x)” is :
Find the domain of the function given by :
The argument (input to the function) of logarithmic function is addition of two square roots. We need to find values of “x” such that the argument of the logarithmic function evaluates to a positive number. An unsigned square root is a positive number by definition. It can not be negative. Symbolically, √x is a positive number. Clearly, each of the square roots is a positive number. Hence, their addition is also a positive number. Thus, we see that the requirement of the argument of a logarithmic function being a positive number, is automatically fulfilled by virtue of the property of an unsigned square root.
We, therefore, only need to evaluate “x” for which each of the square roots is real. In other words, the expressions in each of the square roots is a non-negative integer.
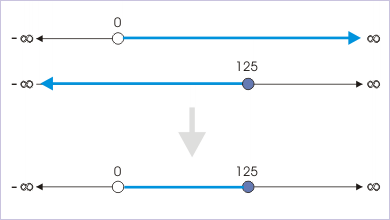
The two square root functions are added to form the argument of logarithmic function. We know that domain of function resulting from addition is intersection of domains of individual square root function. Hence,
Find the domain of the function :
Hints : There are two logarithmic functions composing the given function. Let us call them outer and inner. For outer logarithmic function,
For inner logarithmic function,
Here, coefficient of squared term is positive and and D<0. Hence, this inequality is true for all real x i.e. xR. Now, domain of given function is intersection of two intervals.
Problem 3 : Find the domain of the function given by :
The function is formed by nesting three logarithmic functions. Further base of logarithmic functions are different. For determining domain we (i) find value of “x” for which “ ” is real (ii) find range of “ ” for which “ ” is real and (iii) find range of “ ” for which f(x) is real.
For “ ” to be real, x is a positive number. It means,
For “ ” to be real, “ ” is required to be positive. It means,
Using the fact that , we have :
For “f(x)” to be real, “ ” is required to be positive. It means,
Combining three intervals so obtained,
Domain of the function

Find the range of the function :
Hints : We need to find minimum and maximum value of logarithmic function for the values of x in domain of the function. The argument of logarithmic function is a quadratic function, whose coefficient of squared term is positive and D<0. It means its graph is a parabola opening up in the positive side of y-axis. The minimum value of the quadratic expression is :
Now, we know that graph of logarithmic function for base, a>1, is a continuously increasing graph. It means that value of logarithmic function, corresponding to min and max values of quadratic expression is the range of given function.
Hence, range of given function is :
Find domain and range if
Rearranging, we have :
Taking logarithm on either sides of equation,
For logarithmic function,
In order to find range, we solve function expression for y. In exponential form,
Taking logarithm on either sides of equation,
For logarithmic function,

Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?