0.3 5.4 gravitational potential energy  (Page 3/4)

Finding the speed of a roller coaster from its height

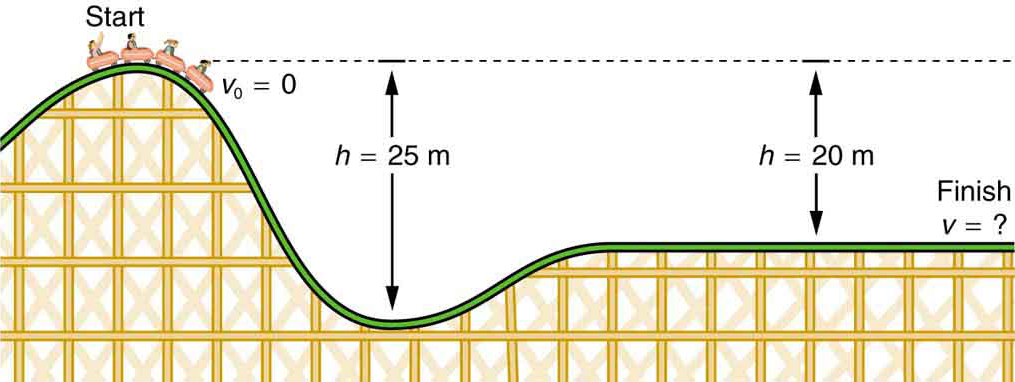
(a) What is the final speed of the roller coaster shown in [link] if it starts from rest at the top of the 20.0 m hill and work done by frictional forces is negligible? (b) What is its final speed (again assuming negligible friction) if its initial speed is 5.00 m/s?

Strategy

The roller coaster loses potential energy as it goes downhill. We neglect friction, so that the remaining force exerted by the track is the normal force, which is perpendicular to the direction of motion and does no work. The net work on the roller coaster is then done by gravity alone. The loss of gravitational potential energy from moving downward through a distance $h$ equals the gain in kinetic energy. This can be written in equation form as $-\text{Δ}{\text{PE}}_{\text{g}}=\text{Δ}\text{KE}$ . Using the equations for ${\text{PE}}_{\text{g}}$ and $\text{KE}$ , we can solve for the final speed $v$ , which is the desired quantity.

Solution for (a)

Here the initial kinetic energy is zero, so that $\text{ΔKE}=\frac{1}{2}{\text{mv}}^2$ . The equation for change in potential energy states that ${\text{ΔPE}}_{\text{g}}=\text{mgh}$ . Since $h$ is negative in this case, we will rewrite this as ${\text{ΔPE}}_{\text{g}}=-\text{mg}\mid h\mid$ to show the minus sign clearly. Thus,

becomes

Solving for $v$ , we find that mass cancels and that

Substituting known values,

Solution for (b)

Again $-{\text{ΔPE}}_{\text{g}}=\text{ΔKE}$ . In this case there is initial kinetic energy, so $\text{ΔKE}=\frac{1}{2}m{v}^2-\frac{1}{2}m{v_0}^2$ . Thus,

Rearranging gives

This means that the final kinetic energy is the sum of the initial kinetic energy and the gravitational potential energy. Mass again cancels, and

This equation is very similar to the kinematics equation $v=\sqrt{{v_0}^2+2\text{ad}}$ , but it is more general—the kinematics equation is valid only for constant acceleration, whereas our equation above is valid for any path regardless of whether the object moves with a constant acceleration. Now, substituting known values gives

Discussion and Implications

First, note that mass cancels. This is quite consistent with observations made in Falling Objects that all objects fall at the same rate if friction is negligible. Second, only the speed of the roller coaster is considered; there is no information about its direction at any point. This reveals another general truth. When friction is negligible, the speed of a falling body depends only on its initial speed and height, and not on its mass or the path taken. For example, the roller coaster will have the same final speed whether it falls 20.0 m straight down or takes a more complicated path like the one in the figure. Third, and perhaps unexpectedly, the final speed in part (b) is greater than in part (a), but by far less than 5.00 m/s. Finally, note that speed can be found at any height along the way by simply using the appropriate value of $h$ at the point of interest.

We have seen that work done by or against the gravitational force depends only on the starting and ending points, and not on the path between, allowing us to define the simplifying concept of gravitational potential energy. We can do the same thing for a few other forces, and we will see that this leads to a formal definition of the law of conservation of energy.

Section summary

• Work done against gravity in lifting an object becomes potential energy of the object-Earth system.
• The change in gravitational potential energy, $\mathrm{\Delta }{\text{PE}}_{\text{g}}$ , is ${\text{ΔPE}}_{\mathrm{g}}=\text{mgh}$ , with $h$ being the increase in height and $\mathrm{g}$ the acceleration due to gravity.
• The gravitational potential energy of an object near Earth’s surface is due to its position in the mass-Earth system. Only differences in gravitational potential energy, ${\text{ΔPE}}_{\mathrm{g}}$ , have physical significance.
• As an object descends without friction, its gravitational potential energy changes into kinetic energy corresponding to increasing speed, so that $\text{ΔKE}\text{= −}{\text{ΔPE}}_{\text{g}}$ .

Conceptual questions

Problems&Exercises

A hydroelectric power facility (see [link] ) converts the gravitational potential energy of water behind a dam to electric energy. (a) What is the gravitational potential energy relative to the generators of a lake of volume $\text{50}\text{.}\mathrm{0\; k}{\text{m}}^3$ ( $\text{mass}=5\text{.}\text{00}\times {\text{10}}^{\text{13}}\text{kg})$ , given that the lake has an average height of 40.0 m above the generators?

(a) $1\text{.}\text{96}\times {\text{10}}^{\text{16}}\text{J}$

A 100-g toy car is propelled by a compressed spring that starts it moving. The car follows the curved track in [link] . Show that the final speed of the toy car is 0.687 m/s if its initial speed is 2.00 m/s and it coasts up the frictionless slope, gaining 0.180 m in altitude.

$v_f=\sqrt{2\text{gh}+{v_0}^2}=\sqrt{2(\text{9.80 m}{\text{/s}}^2)(-0\text{.180 m})+(2\text{.00 m/s}{)}^2}=0\text{.687 m/s}$