2.3 Properties of the real numbers  (Page 2/2)

Practice set b

Fill in the $(\begin{array}{cc}& \end{array})$ to make each statement true. Use the associative properties.

Sample set c

Practice set c

Simplify each of the following quantities.

The distributive properties

When we were first introduced to multiplication we saw that it was developed as a description for repeated addition.

$4+4+4=3\cdot 4$

Notice that there are three 4’s, that is, 4 appears 3 times . Hence, 3 times 4.
We know that algebra is generalized arithmetic. We can now make an important generalization.

When a number $a$ is added repeatedly $n$ times, we have
$\underset{a\text{appears}n\text{times}}{\underbrace{a+a+a+\cdots +a}}$
Then, using multiplication as a description for repeated addition, we can replace
$\begin{array}{ccc}\underset{n\text{times}}{\underbrace{a+a+a+\cdots +a}}& \text{with}& na\end{array}$

For example:

The distributive property involves both multiplication and addition. Let’s rewrite $4(a+b).$ We proceed by reading $4(a+b)$ as a multiplication: 4 times the quantity $(a+b)$ . This directs us to write

$\begin{array}{lll}4(a+b)\hfill & =\hfill & (a+b)+(a+b)+(a+b)+(a+b)\hfill \\ \hfill & =\hfill & a+b+a+b+a+b+a+b\hfill \end{array}$

Now we use the commutative property of addition to collect all the $a\text{'}s$ together and all the $b\text{'}s$ together.

$\begin{array}{lll}4(a+b)\hfill & =\hfill & \underset{4a\text{'}s}{\underbrace{a+a+a+a}}+\underset{4b\text{'}s}{\underbrace{b+b+b+b}}\hfill \end{array}$

Now, using multiplication as a description for repeated addition, we have

$\begin{array}{lll}4(a+b)\hfill & =\hfill & 4a+4b\hfill \end{array}$

We have distributed the 4 over the sum to both $a$ and $b$ .

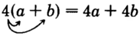
The distributive property

The distributive property is useful when we cannot or do not wish to perform operations inside parentheses.

Sample set d

Use the distributive property to rewrite each of the following quantities.

Practice set d

Use the distributive property to rewrite each of the following quantities.

The identity properties

Additive identity

Multiplicative identity

We summarize the identity properties as follows.

$\begin{array}{cc}\begin{array}{l}\text{ADDITIVE}\text{IDENTITY}\\ \text{PROPERTY}\end{array}& \begin{array}{l}\text{MULTIPLICATIVE}\text{IDENTITY}\\ \text{}\text{}\text{}\text{}\text{}\text{PROPERTY}\end{array}\\ \text{If}a\text{is}\text{a}\text{real}\text{number,\hspace{0.17em}then}& \text{If}a\text{is}\text{a}\text{real}\text{number,}\text{then}\\ a+0=a\text{and}0+a=a& a\cdot 1=a\text{and}1\cdot a=a\end{array}$

The inverse properties

Additive inverses

Multiplicative inverses

We summarize the inverse properties as follows.

The inverse properties

1. If $a$ is any real number, then there is a unique real number $-a$ , such that
   $\begin{array}{ccc}a+(-a)=0& \text{and}& -a+a=0\end{array}$
   The numbers $a$ and $-a$ are called additive inverses of each other.
2. If $a$ is any nonzero real number, then there is a unique real number $\frac{1}{a}$ such that
   $\begin{array}{ccc}a\cdot \frac{1}{a}=1& \text{and}& \frac{1}{a}\end{array}\cdot a=1$
   The numbers $a$ and $\frac{1}{a}$ are called multiplicative inverses of each other.

Expanding quantities

Exercises

Use the commutative property of addition and multiplication to write expressions for an equal number for the following problems. You need not perform any calculations.

Simplify using the commutative property of multiplication for the following problems. You need not use the distributive property.

For the following problems, use the distributive property to expand the quantities.

Exercises for review