| << Chapter < Page | Chapter >> Page > |
Use your
Pgram function
to estimate the power spectrumof
,
.
Plot
vs.
.
Next, estimate the power spectrum of , using of the samples of . Do this only using samples , , , . Plot vs. .
Pgram code.The periodogram is a simple method, but it does not yield very good results.To get a better estimate of the power spectrum, we will introduce Bartlett's method, also known as the averaged periodogram . This method has three steps. Suppose we have a length-N sequence .
Write a Matlab function called
AvPgram to calculate
the averaged periodogram, using the above steps.The syntax for this function should be
[P,w] = AvPgram(x, K)
where
is a discrete random sequence of length
and
the
is the number of nonoverlapping segments. The
outputs of this command are
, the samples of the averaged periodogram,
and
, the corresponding frequencies of the samples. Both
and
should be vectors of length M where N=KM.
You may use your
Pgram function.
A=reshape(x,M,K) will orient length
segments of the vector
into
columns of the matrix
.Use your Matlab function
AvPgram to estimate the power
spectrum of
which was generated in the previous section.
Use all 1024 samples of
, and let
. Plot
vs.
.
AvPgram code.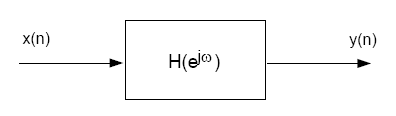
Consider a linear time-invariant system with frequency response , where is the power spectrum of the input signal, and is the power spectrum of the output signal.It can be shown that these quantities are related by
In the "Periodogram" section, the sequence was generated byfiltering an i.i.d. Gaussian (mean=0, variance=1) sequence , using the filter in [link] . By hand, calculate the power spectrum of , the frequency response of the filter, , and the power spectrum of .
Download the file speech.au for this section. For help on the following Matlab topics select the corresponding link: how to load and play audio signals and specgram function .
The methods used in the last two sections can only be applied to stationary random processes. However, most signals in nature are not stationary. For a nonstationary random process,one way to analyze it is to subdivide the signal into segments (which may be overlapping)and treat each segment as a stationary process. Then we can calculate the power spectrum of each segment. This yieldswhat we call a spectrogram .
While it is debatable whether or not a speech signal is actually random,
in many applications it is necessary to model it as being so.In this section, you are going to use the Matlab command
specgram to calculate the spectrogram of a speech signal. Read the help for the
specgram function .
Find out what the command does, and how to calculate and draw aspectrogram.
Draw the spectrogram of the speech signal in
speech.au .
When using the
specgram command with no output arguments,
the absolute value of the spectrogram will be plotted.Therefore you can use
speech=auread('speech.au');
to read the speech signal and use
specgram(speech);
to draw the spectrogram.

Notification Switch
Would you like to follow the 'Purdue digital signal processing labs (ece 438)' conversation and receive update notifications?