| << Chapter < Page | Chapter >> Page > |
As bases, we choose . with the same coordinate vector in . Further, because of and , with the same coordinate vector. Thus, in matrix form is the so-called butterfly matrix, which is a DFT of size 2: .
Assume has pairwise distinct zeros . Then the CRT can be used to completelydecompose into its spectrum :
If we choose a basis in and bases in each , then , as a linear mapping, is represented by a matrix. The matrix is obtained by mappingevery basis element , , and collecting the results in the columns of the matrix. The result is
and is called the polynomial transform for with basis .
If, in general, we choose as spectral basis, then the matrix corresponding to the decomposition [link] is the scaled polynomial transform
where denotes a diagonal matrix with diagonal entries .
We jointly refer to polynomial transforms, scaled or not, as Fourier transforms.
We show that the is a polynomial transform for with basis . Namely,
which means that takes the form
The associated polynomial transform hence becomes
This interpretation of the DFT has been known at least since [link] , [link] and clarifies the connection between the evaluation points in [link] and the circular convolution in [link] .
In [link] , DFTs of types 1–4 are defined, with type 1 being the standard DFT. In the algebraic framework, type 3 is obtainedby choosing as algebra with the same basis as before:
The DFTs of type 2 and 4 are scaled polynomial transforms [link] .
Knowing the polynomial algebra underlying the DFT enables us to derive the Cooley-Tukey FFT algebraically . This means that instead of manipulating the DFT definition, we manipulate the polynomial algebra . The basic idea is intuitive. We showed that the DFT is the matrix representation of the complete decomposition [link] . The Cooley-Tukey FFT is now derived by performing this decomposition in steps as shown in [link] . Each step yields a sparse matrix; hence, the is factorized into a product of sparse matrices, which will be the matrix representation ofthe Cooley-Tukey FFT.
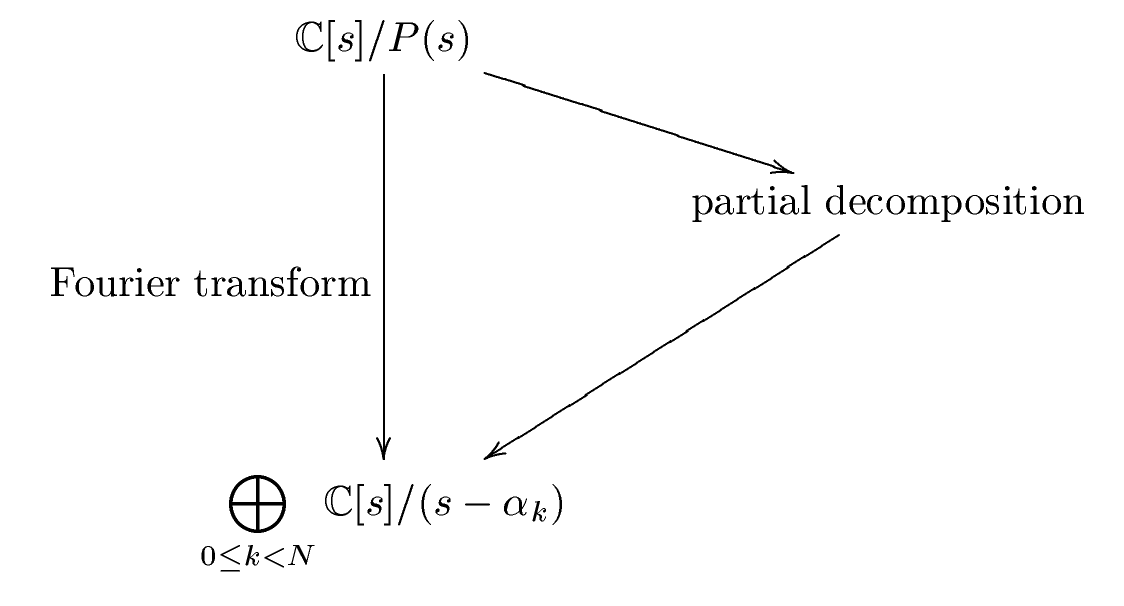
This stepwise decomposition can be formulated generically for polynomial transforms [link] , [link] . Here, we consider only the DFT.
We first introduce the matrix notation we will use and in particular the Kronecker product formalism that became mainstream for FFTsin [link] , [link] .
Then we first derive the radix-2 FFT using a factorization of . Subsequently, we obtain the general-radix FFT using a decomposition of .

Notification Switch
Would you like to follow the 'Fast fourier transforms' conversation and receive update notifications?