| << Chapter < Page | Chapter >> Page > |
An emergency room at a particular hospital gets an average of five patients per hour. A doctor wants to know the probability that the ER gets more than five patients per hour. Give the reason why this would be a Poisson distribution.
This problem wants to find the probability of events occurring in a fixed interval of time with a known average rate. The events are independent.
X ~ P ( μ )
Read this as " X is a random variable with a Poisson distribution." The parameter is μ (or λ ); μ (or λ ) = the mean for the interval of interest.
P ( X = x ) =
Leah's answering machine receives about six telephone calls between 8 a.m. and 10 a.m. What is the probability that
Let X = the number of calls Leah receives in 15 minutes. (The interval of interest is 15 minutes or hour.)
x = 0, 1, 2, 3, ...
If Leah receives, on the average, six telephone calls in two hours, and there are eight 15 minute intervals in two hours, then Leah receives
(6) = 0.75 calls in 15 minutes, on average. So, μ = 0.75 for this problem.
X ~ P (0.75)
The TI calculators use λ (lambda) for the mean.
The probability that Leah receives more than one telephone call in the next 15 minutes is about 0.1734:
P (
x >1) = 1 − poissoncdf(0.75, 1).
The graph of X ~ P (0.75) is:
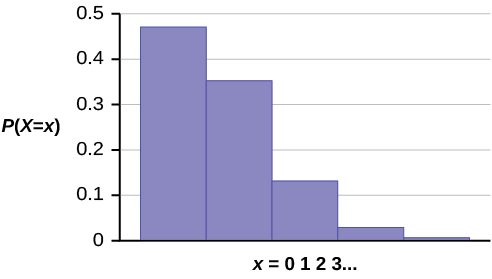
The y -axis contains the probability of x where X = the number of calls in 15 minutes.
A customer service center receives about ten emails every half-hour. What is the probability that the customer service center receives
For this problem we want the average per 6 minutes. If the average is ten per 30 minutes, then in 6 minutes we would expect two emails. μ = 2 per 6 minutes.
According to Baydin, an email management company, an email user gets, on average, 147 emails per day. Let X = the number of emails an email user receives per day. The discrete random variable X takes on the values x = 0, 1, 2 …. The random variable X has a Poisson distribution: X ~ P (147). The mean is 147 emails.
According to a recent poll by the Pew Internet Project, girls between the ages of 14 and 17 send an average of 187 text messages each day. Let X = the number of texts that a girl aged 14 to 17 sends per day. The discrete random variable X takes on the values X = 0, 1, 2 …. The random variable X has a Poisson distribution: X ~ P (187). The mean is 187 text messages.

Notification Switch
Would you like to follow the 'Introduction to statistics i - stat 213 - university of calgary - ver2015revb' conversation and receive update notifications?