| << Chapter < Page | Chapter >> Page > |
where α t is determined by the degree of stopband rejection desired Specifically, , where SBR is the minimum stopband rejection in decibels. A typical value for SBR is 60 dB, yielding an α t of 2.42. and is the tuner's transition band. In this case, the transition band can be no greater than the difference between B t and f s . If we assume the use of this limiting value, L t is given by
Substituting this expression and expressing all sampling rates in terms of the input rate produces an equation for the total number of multiply-adds required.
Another useful form of this equation makes the functional dependence on f s more explicit. We do this by using the expressions
and the assumption that a radix-2 FFT is employed to compute the DFT. With these, the expression for the total number of multiply-adds can be written as
Given expressions such as those shown in [link] and [link] it is possible to accurately estimate the total amount of multiply-add computation needed for a tuner/transmux processor. It is also possible to perform tradeoffs between the various parameters in order to optimize the resulting design. While this can in principle be done with any of the design parameters, we demonstrate in this section the computational implications of varying the parameter f s , the input sampling rate to the transmultiplexer. In practice, this usually turns out to be one of the designer's most important parameter choices.
[link] shows the computational requirements for a hypothetical transmultiplexer. In this case, the input sampling rate is assumed to be 6.4 MHz. The tuner must select an FDM telephone supergroup from the input signal and demultiplex all 60 voice channels in the supergroup. The tuner's bandwidth B t must therefore be greater than or equal to 240 kHz and f s must exceed that. For the telephone demultiplexing application, the channel spacing is usually 4 kHz and the over-sampling factor K is typically chosen to be unity. [link] shows five curves, one for each segment of the computation and one for the composite. The number of multiply-adds required by the input mixer is constant, since the input sampling rate is fixed. The computation required by the tuner's filter falls as f s rises from 240 kHz and tends toward the input Nyquist frequency of 3.2 MHz. The cause of this can be ascertained by examining [link] . As f s decreases toward B t , the transition band decreases, L t increases hyperbolically, and the amount of computation needed for the tuner's filter grows without bound.
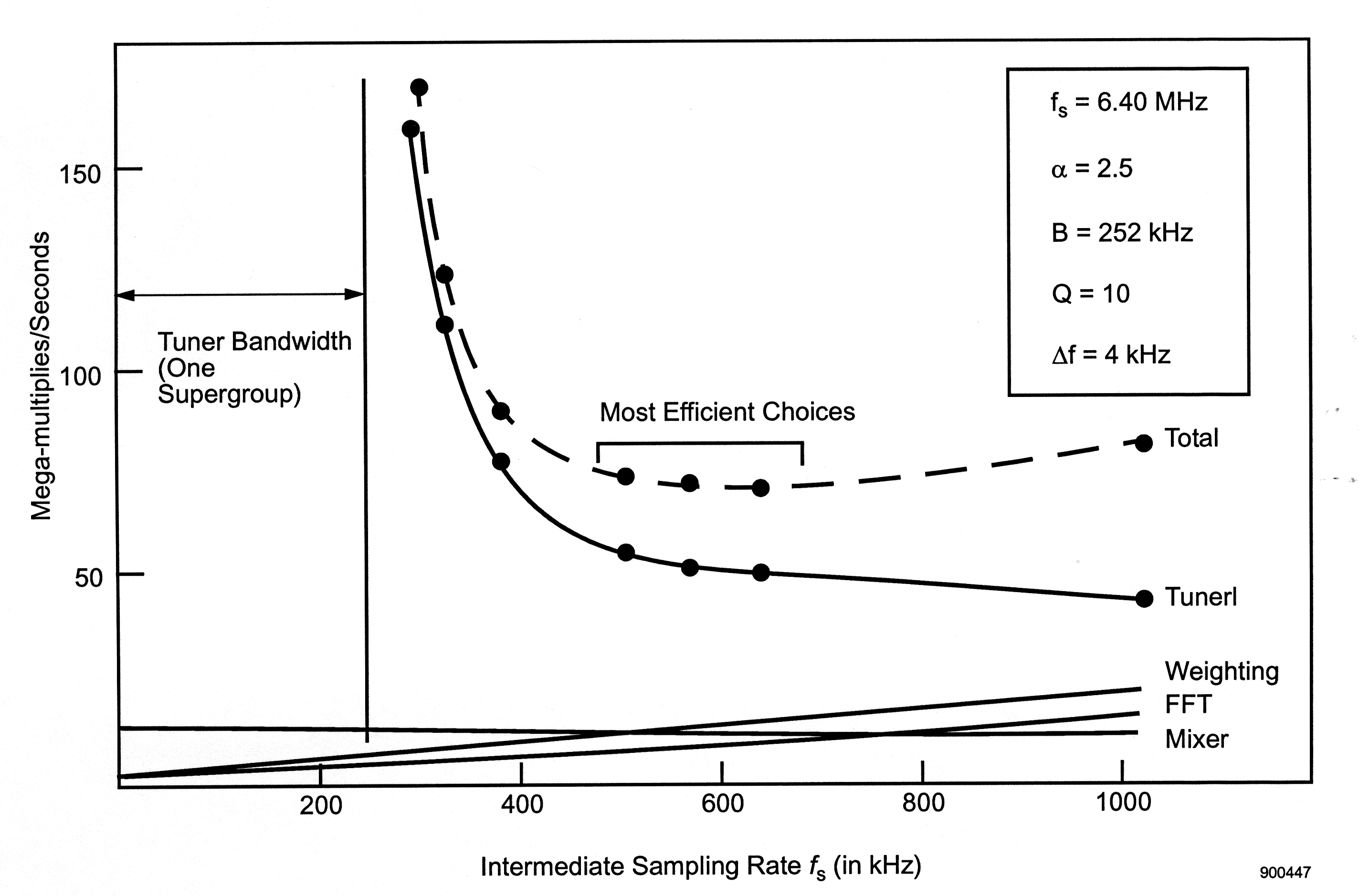
The next two curves describe the effect of f s on the two components of the transmultiplexer. For a given value of Q , the computation required by the preprocessor is strictly proportional to f s . The FFT's computation rises slightly faster than proportionally since the number of FFT bins grows as f s does. The sum of these constituent curves represents the total amount of multiply-add computation needed. Note that it has a broad minimum. It rises precipitously as f s decreases toward B t and more slowly as f s increases toward its other limit .

Notification Switch
Would you like to follow the 'An introduction to the fdm-tdm digital transmultiplexer' conversation and receive update notifications?