0.17 Phase equilibrium in solutions  (Page 6/9)

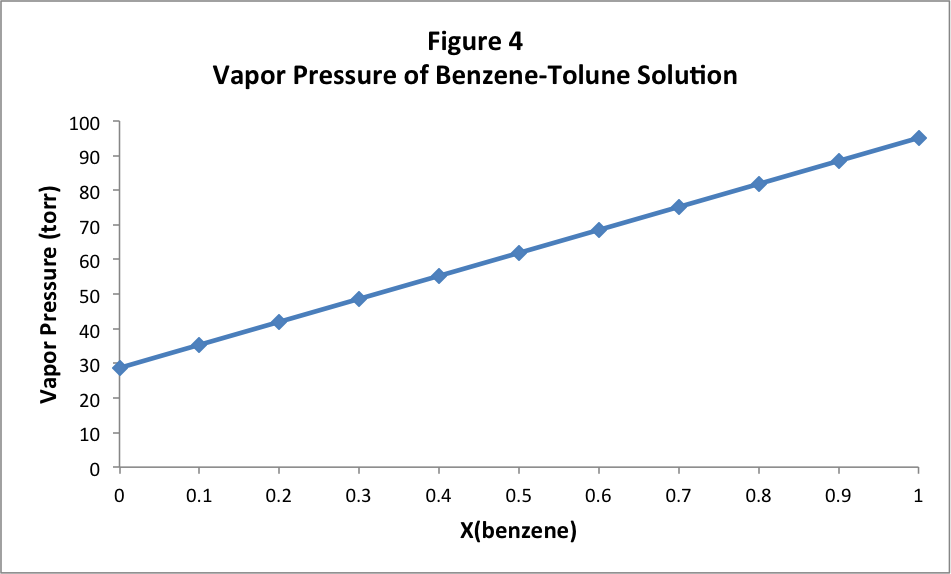
We get a very simple linear relationship, increasing from the vapor pressure of pure toluene, when the mole fraction of benzene is 0, to the vapor pressure of pure benzene, when the mole fraction of benzene is 1. The equation for this straight line can be found simply to be:

P _vap =P ^* _toluene +(P ^* _benzene -P ^* _tolune )X _benzene

Where P _vap is the observed vapor pressure above the solution, and P ^* is the vapor pressure of either pure toluene or pure benzene. We can slightly rearrange this equation by separating the benzene terms from the toluene terms and using the fact that X _benzene = 1 – X ^* _toluene :

P _vap = P ^* _toluene + P ^* _benzene X _benzene - P ^* _tolune X _benzene

P _vap = P ^* _toluene + P ^* _benzene X _benzene - P ^* _tolune (1 - X _toluene )

P _vap = P ^* _benzene X _benzene + P ^* _tolune X _toluene

Recall Raoult’s law from earlier in this study, which generally states that P _vap =P ^* _vap *X _solvent . Both terms in the last equation above look just like Raoult’s law for each component. This means that each component is contributing to the total vapor pressure of the solution exactly by what we would have expected it to contribute if it were the only volatile component of the solution. And the two vapor pressures add together simply just as we would have expected from Dalton’s Law of Partial Pressures, which is a result of the Ideal Gas Law.

When two liquids mix in solution to combine their vapor pressures in this very simple way, we call the solution “ideal.” Generally, we observe this ideal behavior when the two components of the solution have molecules that have similar intermolecular forces.

We can understand this experimental result by thinking about dynamic equilibrium. In order for the solution to be in equilibrium with the vapor, each component must be in dynamic equilibrium. Each component lowers the rate of evaporation of the other component in the same way that a nonvolatile solute lowers the rate of evaporation of the solvent. Therefore, each component has a lower number of molecules in the vapor phase to balance the dynamic equilibrium. And the two components’ vapor pressures add together to form the total solution vapor pressure because, at these low pressure, the kinetic molecular theory accurately describes the gas phase, so the Ideal Gas Law and Dalton’s Law apply.

Observation 3: equilibrium between solids and liquid solutions

So far, we have only examined liquid-vapor equilibrium and the effects on that equilibrium by the presence of a solute in the liquid phase. However, we can easily observe that a solute in the liquid solvent also disrupts the equilibrium between the liquid solvent and its solid phase. The most prevalent observation of this involves the freezing of salt water. It has long been common practice in cold climates on icy days to spread salt over ice covered streets and sidewalks. This serves to melt the ice, despite the fact that the temperature of the air is below 0 ºC. The added salt disrupts the normal solid-liquid equilibrium, allowing the ice to melt at temperatures below 0 ºC. This means that the presence of the salt in the water lowers the freezing point of the water. Experimentally, we find that the freezing point of water is lowered by over 20 ºC for a saturated salt solution. The lowering of the freezing point is a much larger effect than the elevation of the boiling point.