| << Chapter < Page | Chapter >> Page > |
The net drift velocity in a conductor is zero unless an electric potential difference is applied to the conductor. If we move the conductor strip in a uniform magnetic field, then free or conduction electrons acquire relative velocity with respect to stationary magnetic field. This, in turn, would set up a magnetic force on the conduction electrons. Clearly, the action to move conductor strip in the magnetic field is equivalent to imparting a net drift velocity to the conduction electrons.
Motion of a conductor strip in magnetic field
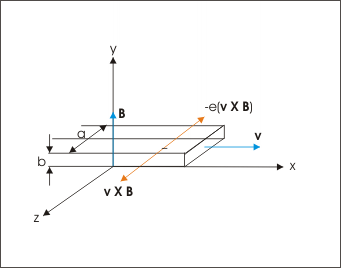
Let us consider a metallic strip of width “a” and thickness “b” moving in x-direction as shown in the figure with a velocity “v”. Also let the magnetic field is in the y-direction. Applying Right hand rule, we see that “ v X B ” is directed in z-direction and “-e( v X B )” is directed in negative z-direction. As a result, one edge is negatively charged and the other edge is positively charged. At equilibrium,
Polarization of charges and electric field

and potential difference across the edge is :
In the case of a thin wire, there is no room for electrons to move sideways as in the case of wide strip of conductor. The sideway motion thus produces a thrust on the wire and there is a net magnetic force on the wire. It is evident that we need to account for magnetic force on each of the free conduction electrons. Since each of these forces is transverse to the straight wire, the direction of net force is same as that of the magnetic force working on any of the conduction electrons. This fact allows us to simply add individual forces arithmetically to determine the resultant force. Further, the net force on wire will also depend on the length of wire being considered as the numbers of free electrons is proportional to the length of wire.
According to Lorentz law the magnetic force on a single electron :
Net magnetic force on the wire
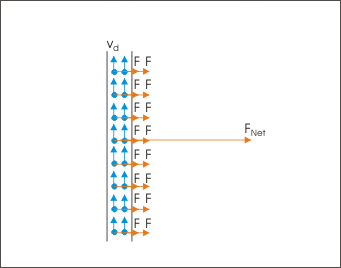
where θ is the angle between magnetic field and drift velocity. Let there be “n” electrons per unit volume. Also, let “L” and “A” be the length and cross section respectively of the wire under consideration. Clearly, the total numbers of electrons in the length “L” of the wire is :
Hence, total magnetic force on the wire of length "L" is :
But we know that :
Substituting, we have :
In vector form, this is written using concept of cross vector product as :
The direction of length vector is same as that of the direction of current in wire.
If the wire under consideration is not a straight wire, then we can not use the expression formulated above. It is important to understand here that the above expression is valid for a straight wire. This is the basic assumption which allowed us to carry out arithmetic sum of individual forces as directions of magnetic forces on individual electrons were same. However, if the wire is not straight, then it would not be possible to do the arithmetic sum for obtaining the resultant force as the directions of magnetic force would be different.

Notification Switch
Would you like to follow the 'Electricity and magnetism' conversation and receive update notifications?