1. Home
  2. Siyavula textbooks: grade 11
  3. Vectors
  4. Adding and subtracting vectors

10.2 Adding and subtracting vectors  (Page 4/4)

<< Chapter < Page
  Siyavula textbooks: grade 11     Page 4 / 4
Chapter >> Page >

Resultant vectors

  1. Harold walks to school by walking 600 m Northeast and then 500 m N 40 ∘ W. Determine his resultant displacement by using accurate scale drawings.
  2. A dove flies from her nest, looking for food for her chick. She flies at a velocity of 2 m · s - 1 on a bearing of 135 ∘ and then at a velocity of 1,2 m · s - 1 on a bearing of 230 ∘ . Calculate her resultant velocity by using accurate scale drawings.
  3. A squash ball is dropped to the floor with an initial velocity of 2,5 m · s - 1 . It rebounds (comes back up) with a velocity of 0,5 m · s - 1 .
    1. What is the change in velocity of the squash ball?
    2. What is the resultant velocity of the squash ball?

Remember that the technique of addition and subtraction just discussed can only be applied to vectors acting along a straight line. When vectors are not in a straight line, i.e. at an angle to each other, the following method can be used:

A more general algebraic technique

Simple geometric and trigonometric techniques can be used to find resultant vectors.

A man walks 40 m East, then 30 m North. Calculate the man's resultant displacement.

  1. As before, the rough sketch looks as follows:

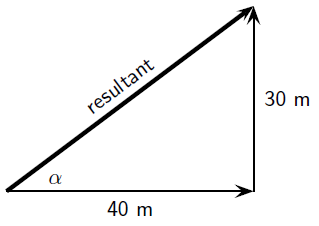
  2. Note that the triangle formed by his separate displacement vectors and his resultant displacement vector is a right-angle triangle. We can thus use the Theorem of Pythagoras to determine the length of the resultant. Let x R represent the length of the resultant vector. Then:

    x R 2 = ( 40 m · s - 1 ) 2 + ( 30 m · s - 1 ) 2 x R 2 = 2 500 m · s - 1 2 x R = 50 m · s - 1

  3. Now we have the length of the resultant displacement vector but not yet its direction. To determine its direction we calculate the angle α between the resultant displacement vector and East, by using simple trigonometry:

    tan α = opposite side adjacent side tan α = 30 40 α = tan - 1 ( 0 , 75 ) α = 36 , 9 ∘

  4. The resultant displacement is then 50 m at 36,9 ∘ North of East.

    This is exactly the same answer we arrived at after drawing a scale diagram!

Got questions? Get instant answers now!

In the previous example we were able to use simple trigonometry to calculate the resultant displacement. This was possible since thedirections of motion were perpendicular (north and east). Algebraic techniques, however, are not limited to cases where the vectors to be combined are along the same straight line or at right angles to oneanother. The following example illustrates this.

A man walks from point A to point B which is 12 km away on a bearing of 45 ∘ . From point B the man walks a further 8 km east to point C. Calculate the resultant displacement.

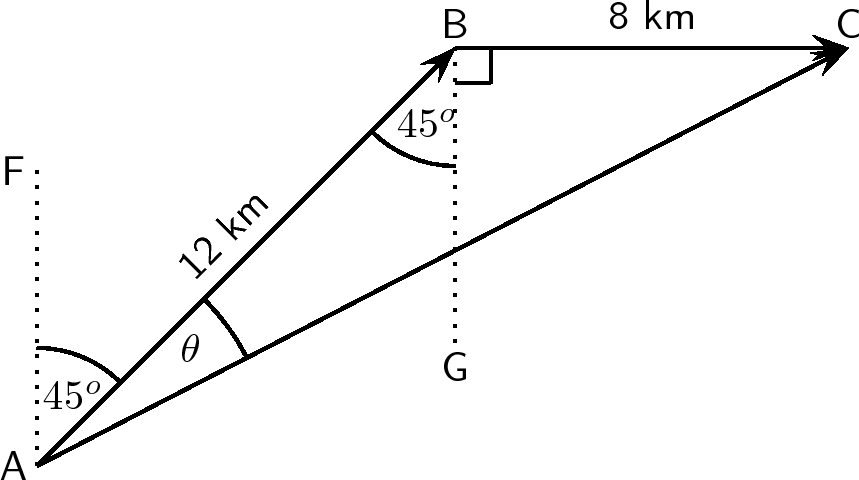
  1. B A ^ F = 45 ∘ since the man walks initially on a bearing of 45 ∘ . Then, A B ^ G = B A ^ F = 45 ∘ (parallel lines, alternate angles). Both of these angles are included in the rough sketch.

  2. The resultant is the vector AC. Since we know both the lengths of AB and BC and the included angle A B ^ C , we can use the cosine rule:

    A C 2 = A B 2 + B C 2 - 2 · A B · B C cos ( A B ^ C ) = ( 12 ) 2 + ( 8 ) 2 - 2 · ( 12 ) ( 8 ) cos ( 135 ∘ ) = 343 , 8 A C = 18 , 5 km

  3. Next we use the sine rule to determine the angle θ :

    sin θ 8 = sin 135 ∘ 18 , 5 sin θ = 8 × sin 135 ∘ 18 , 5 θ = sin - 1 ( 0 , 3058 ) θ = 17 , 8 ∘

    To find F A ^ C , we add 45 ∘ . Thus, F A ^ C = 62 , 8 ∘ .

  4. The resultant displacement is therefore 18,5 km on a bearing of 062,8 ∘ .

Got questions? Get instant answers now!

More resultant vectors

  1. A frog is trying to cross a river. It swims at 3 m · s - 1 in a northerly direction towards the opposite bank. The water is flowing in a westerly direction at 5 m · s - 1 . Find the frog's resultant velocity by using appropriate calculations. Include a rough sketch of the situation in your answer.
  2. Sandra walks to the shop by walking 500 m Northwest and then 400 m N 30 ∘ E. Determine her resultant displacement by doing appropriate calculations.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Siyavula textbooks: grade 11 physical science. OpenStax CNX. Jul 29, 2011 Download for free at http://cnx.org/content/col11241/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?

Ask