1.2 Add whole numbers

Use addition notation

A college student has a part-time job. Last week he worked $3$ hours on Monday and $4$ hours on Friday. To find the total number of hours he worked last week, he added $3$ and $4.$

The operation of addition combines numbers to get a sum    . The notation we use to find the sum of $3$ and $4$ is:

We read this as three plus four and the result is the sum of three and four. The numbers $3$ and $4$ are called the addends. A math statement that includes numbers and operations is called an expression.

Model addition of whole numbers

Addition is really just counting. We will model addition with $\text{base-10}$ blocks. Remember, a block represents $1$ and a rod represents $10.$ Let’s start by modeling the addition expression we just considered, $3+4.$

Each addend is less than $10,$ so we can use ones blocks.

We start by modeling the first number with 3 blocks.
Then we model the second number with 4 blocks.
Count the total number of blocks.

There are $7$ blocks in all. We use an equal sign $\text{(=)}$ to show the sum. A math sentence that shows that two expressions are equal is called an equation. We have shown that. $3+4=7.$

Model the addition $2+6.$

Solution

$2+6$ means the sum of $2$ and $6$

Each addend is less than 10, so we can use ones blocks.

Model the first number with 2 blocks.
Model the second number with 6 blocks.
Count the total number of blocks	There are $8$ blocks in all, so $2+6=8.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

When the result is $10$ or more ones blocks, we will exchange the $10$ blocks for one rod.

Model the addition $5+8.$

Solution

$5+8$ means the sum of $5$ and $8.$

Each addend is less than 10, se we can use ones blocks.
Model the first number with 5 blocks.
Model the second number with 8 blocks.
Count the result. There are more than 10 blocks so we exchange 10 ones blocks for 1 tens rod.
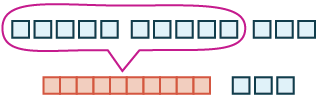Now we have 1 ten and 3 ones, which is 13.	5 + 8 = 13

Notice that we can describe the models as ones blocks and tens rods, or we can simply say ones and tens . From now on, we will use the shorter version but keep in mind that they mean the same thing.

Got questions? Get instant answers now!

Got questions? Get instant answers now!