| << Chapter < Page | Chapter >> Page > |
= - + (5.46)
Để hệ thống cơ trên đây tương đương với mạch RLC nối tiếp của mạch điện.
Với sự tương đương giữa một hệ thống cơ và một hệ thống điện, việc thành lập trực tiếp các phương trình trạng thái cho một hệ thống cơ sẽ trở nên đơn giản.
Nếu ta xem khối lượng thì tương đương với điện cảm, hằng số lò xo K thì tương đương với nghịch đảo của điện dung 1/C .
Vậy có thể chỉ định v(t): vận tốc và fk(t): lực tác động lên lò xo như là các biến số trạng thái. Lý do là cái trước tương tự dòng điện trong cuộn cảm, và cái sau tương tự như điện thế ngang qua tụ.
Do đó phương trình trạng thái của hệ được viết bằng:
Lực trên khối lượng:
(5.47)
Vận tốc của lò xo :
(5.48)
Phương trình trên thì giống như cách viết phương trình điện thế ngang qua 1 cuộn cảm. Còn phương trình dưới giống như phương trình ngang qua tụ.
Thí dụ đơn giản trên cho thấy các phương trình trạng thái và biến số trạng thái của 1 hệ thống động thì không duy nhất.
Thí dụ 5.3:
Xem 1 hệ thống như hình H.5_17a. Vì lò xo bị biến dạng khi chịu tác dụng của lực f(t) hai độ dời y1 và y2 phải được chỉ định cho 2 đầu mút của lò xo. Sơ đồ vật thể tự do của hệ vẽ ở hình H.5_17b.
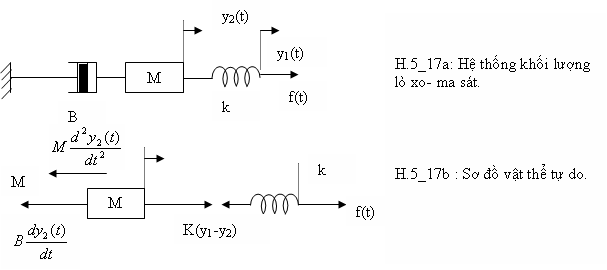
Từ H.5_17b, các phương trình lực được viết :
f(t)=K[y1(t)-y2(t)] (5.49)
(5.50)
Để viết các phương trình trạng thái của hệ thống, ta đặt:
X1(t)=y2(t)
X2(t)=
Thì các phương trình (5.49) và (5.50) được viết lại:
(5.51)
(5.52)
Nếu ta chỉ định vận tốc v(t) của khối lượng M là 1 trạng thái biến số , lực fk(t) trên lò xo là 1 biến số, thì:
(5.53)
fk(t)=f(t) (5.54)
Mạch điện tương đương với hệ cơ trên được vẽ ở hình H.5_18.
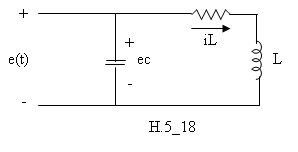
Nếu muốn tìm độ dời y1(t) tại điển mà y(t) áp dụng vào, ta dùng hệ thức:
(5.55)
Trong đó y2(0) là độ dời ban đầu của khối lượng M .
Mặt khác, có thể giải cho y2(t) từ 2 phương trình trạng thái (5.51) và (5.52) và y1(t) được xác định bằng (5.49).
Thí dụ 5.4:
Hệ thống quay vẽ ở hình H.5_19 gồm 1 đầu thì cố định. Moment quán tính của dĩa quanh trục là J. Rìa của dĩa được lướt trên mặt phẳng và hệ số ma sát trượt là B. Bỏ qua quán tính của trục. Hằng số xoắn là K.
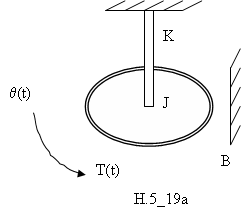
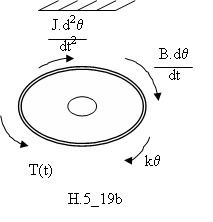
Giả sử 1 moment áp dụng vào hệ thống như hình vẽ:
Phương trình momen quanh trục được viết từ hình H.5_19b
T(t)= (5.62)
Hệ thống này tương tự như hệ thống chuyển động tịnh tiến ở H.5_16. Các phương trình trạng thái có thể viết bằng các định nghĩa các biến. x1(t)=
Và
Ngươì đọc có thể thực hiện các bước tiếp theo để viết phương trình trạng thái như là 1 bài tập.
Motor DC có thể được xếp thành 2 loại : loại có từ thông thay đổi được và loại không có từ thông thay đổi được.
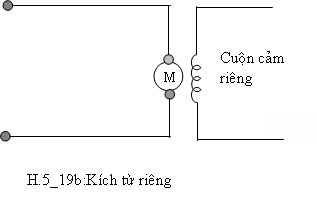
-Trong loại thứ nhất: Từ trường được tạo bởi cuộn cảm. Mà cuộn cảm thì đấu với 1 từ trường ngoài. Loại động cơ này lại được có thể chia làm 2 loại: kích từ nối tiếp và kích từ riêng.
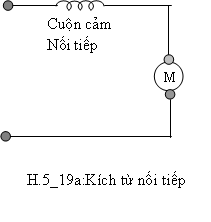
H.5_19a, ký hiệu của động cơ DC kích từ nối tiếp. Cuộn cảm đấu nối tiếp với phần ứng.

Notification Switch
Would you like to follow the 'Cơ sở tự động học' conversation and receive update notifications?