| << Chapter < Page | Chapter >> Page > |
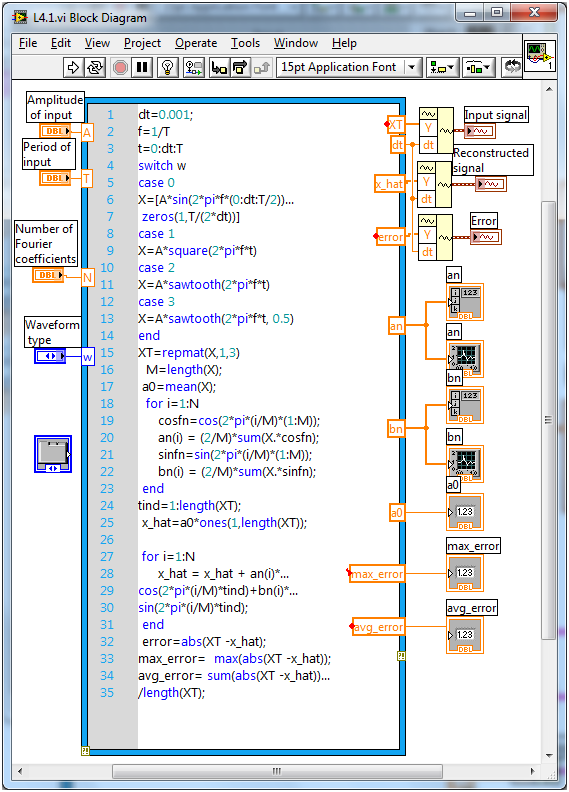
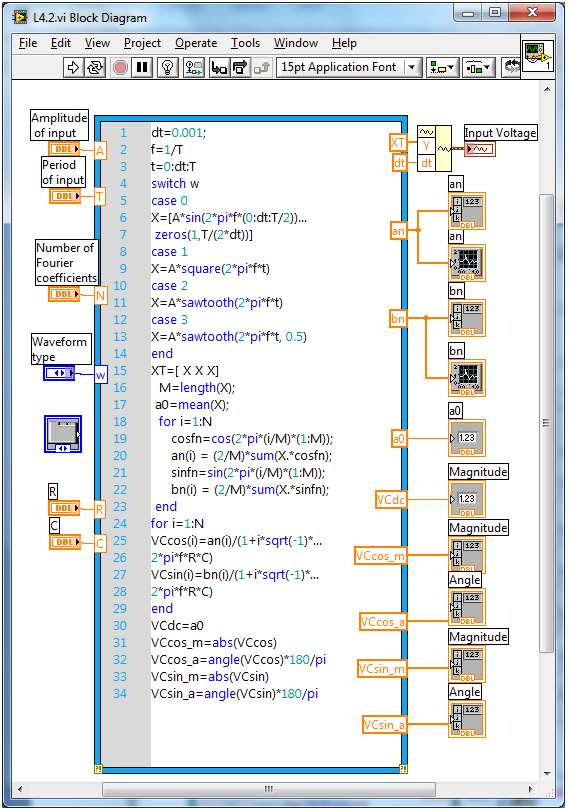
In this example, let us perform electrical circuit analysis using the trigonometric Fourier series. The ability to decompose any periodic signal into a number of sine waves makes the Fourier series a powerful tool in electrical circuit analysis. The response of a circuit component when a sinusoidal input is applied to its terminals is well-known in circuit analysis. Thus, to obtain the response to any periodic signal, one can decompose the signal into sine waves and perform a linear superposition of the sine waves.
Consider a simple RC circuit excited by a periodic input signal as shown in [link] .
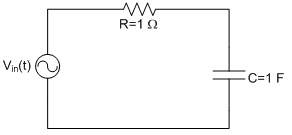
The block diagram of this linear circuit or system is shown in [link] . Determine the Fourier series coefficients of the input voltage signal as discussed in the previous example. Because the Fourier series involves the sum of sinusoids, phasor analysis can be used to obtain the output voltage . Let represent the number of terms in the Fourier series. By using the voltage divider rule, the output voltage can be expressed as [link] ,
Because the sine and cosine components of the input voltage are known, one can easily determine the output by adding the individual output components because the circuit is linear. Determine each output voltage component by using [link] .
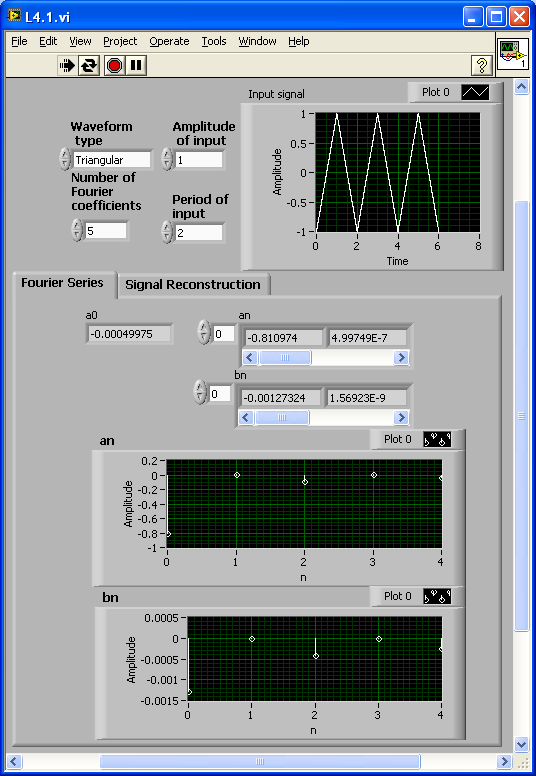
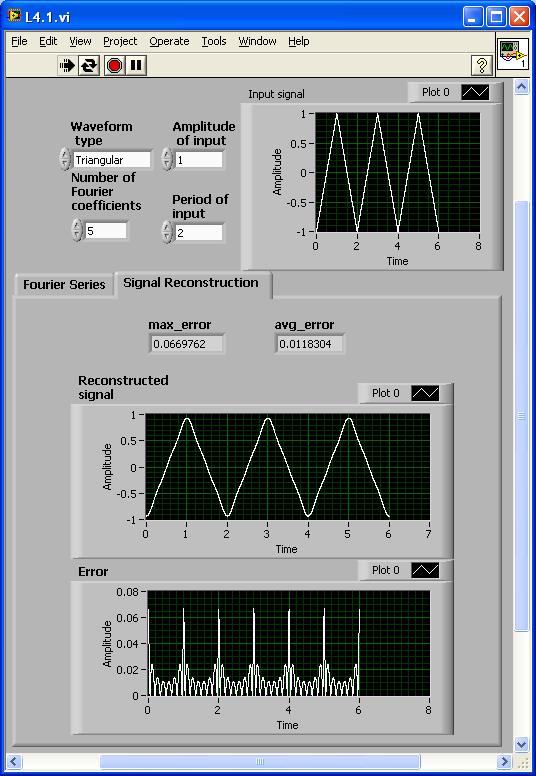
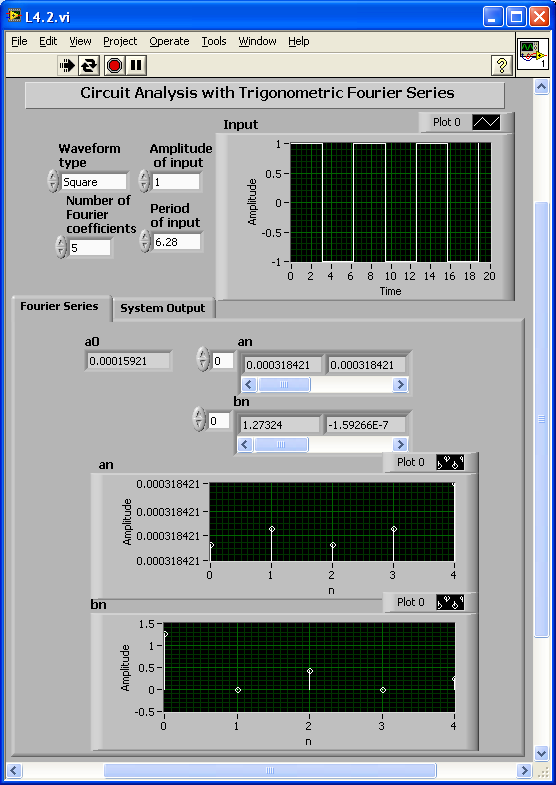
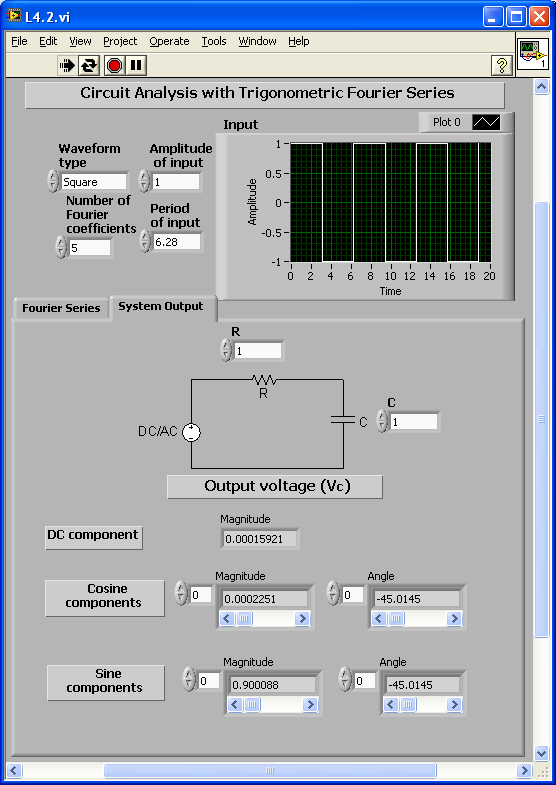
[link] and [link] show the front panel of this system for its two tabs. The magnitude and phase of the sine and cosine components are shown in the front panel separately. Furthermore, the tab control is used to show the Fourier series and system output separately.
RL Circuit Analysis
Build a hybrid VI to analyze the RL circuit shown in [link] using Fourier series.
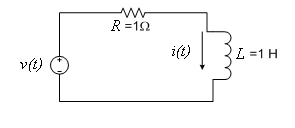
The input voltage for the circuit is to be either a square wave or a triangular wave with a period T=2 seconds.
Compute and display the following:
Hints:
RMS Value
The RMS value of a periodic function with period is given by
The RMS value of a waveform consisting of sinusoids with different frequencies is equal to the square root of the sum of the squares of the RMS value of each sinusoid. If a waveform is represented by the following Fourier series
then, the RMS value is given by
Average power
The average power of the Fourier series can be expressed as
Insert Solution Text Here

Notification Switch
Would you like to follow the 'An interactive approach to signals and systems laboratory' conversation and receive update notifications?