| << Chapter < Page | Chapter >> Page > |
Evaluate the following integrals. If the integral is not convergent, answer “divergent.”
Without integrating, determine whether the integral converges or diverges by comparing the function with
Converges
Without integrating, determine whether the integral converges or diverges.
Determine whether the improper integrals converge or diverge. If possible, determine the value of the integrals that converge.
Determine the convergence of each of the following integrals by comparison with the given integral. If the integral converges, find the number to which it converges.
compare with
Evaluate the integrals. If the integral diverges, answer “diverges.”
Evaluate the improper integrals. Each of these integrals has an infinite discontinuity either at an endpoint or at an interior point of the interval.
Evaluate (Be careful!) (Express your answer using three decimal places.)
Evaluate (Express the answer in exact form.)
Find the area of the region in the first quadrant between the curve and the x -axis.
Find the area of the region bounded by the curve the x -axis, and on the left by
7.0
Find the area under the curve bounded on the left by
Find the volume of the solid generated by revolving about the x -axis the region under the curve from to
Find the volume of the solid generated by revolving about the y -axis the region under the curve in the first quadrant.
Find the volume of the solid generated by revolving about the x -axis the area under the curve in the first quadrant.
The Laplace transform of a continuous function over the interval is defined by (see the Student Project). This definition is used to solve some important initial-value problems in differential equations, as discussed later. The domain of F is the set of all real numbers s such that the improper integral converges. Find the Laplace transform F of each of the following functions and give the domain of F .
Use the formula for arc length to show that the circumference of the circle is
Answers will vary.
A function is a probability density function if it satisfies the following definition: The probability that a random variable x lies between a and b is given by
Show that is a probability density function.
Find the probability that x is between 0 and 0.3. (Use the function defined in the preceding problem.) Use four-place decimal accuracy.
0.8775
For the following exercises, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.
cannot be integrated by parts.
In numerical integration, increasing the number of points decreases the error.
For the following exercises, evaluate the integral using the specified method.
using integration by parts
using integration by parts
using trigonometric substitution
For the following exercises, integrate using whatever method you choose.
For the following exercises, approximate the integrals using the midpoint rule, trapezoidal rule, and Simpson’s rule using four subintervals, rounding to three decimals.
For the following exercises, evaluate the integrals, if possible.
for what values of does this integral converge or diverge?
For the following exercises, consider the gamma function given by
Show that
Extend to show that assuming is a positive integer.
The fastest car in the world, the Bugati Veyron, can reach a top speed of 408 km/h. The graph represents its velocity.
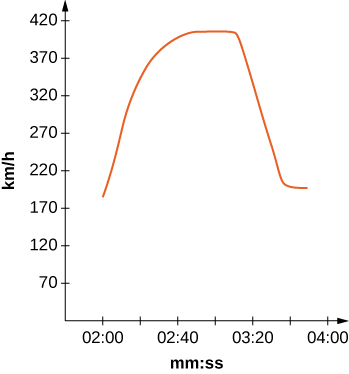
[T] Use the graph to estimate the velocity every 20 sec and fit to a graph of the form ( Hint: Consider the time units.)
[T] Using your function from the previous problem, find exactly how far the Bugati Veyron traveled in the 1 min 40 sec included in the graph.
Answers may vary. Ex: km

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?