Rice university vigre: edge length minimizing polyhedra

Introduction

In the Calculus of Variations PFUG, we studied Melzak's Problem using variational methods. These methods involve the study of geometric objects by defining a functional, which quantitatively measures those objects. We then seek to describe properties of objects which optimize this functional.

For the problem studied, the functional involved the edge length and volume of polyhedra. For a polyhedron $P,$ let $V\left(P\right)$ be its volume and $E\left(P\right)$ be its total edge length. Let $\mathcal{P}$ be the set of all polyhedra P with $V\left(P\right)=1.$ Then Melzak's Problem, which is also referred to as the Waste Storage Problem, asks if there exists a polyhedron $P_0\in \mathcal{P}$ with $E\left(P_0\right)\le E\left(P\right)$ for all $P\in \mathcal{P}.$

As a practical consideration, it is inconvenient to consider polyhedra P with $V\left(P\right)=1,$ namely because easy examples are unwieldy to construct. For example, it is computationally much easier to work with the tetrahedron with unit length edges, having volume $\frac{\sqrt{2}}{12}.$ In order to circumvent this problem, we define

for P any polyhedron. It follows that a polyhedron P minimizes the quantity $\mathcal{F}\left(P\right)$ amongst all polyhedra if and only if the rescaled polyhedron $\tilde{P},$ given by taking the edges e _i of P and setting the new corresponding edge of $\tilde{P}$ to be ${\tilde{e}}_i=\frac{e_i}{V{\left(P\right)}^{1/3}},$ solves Melzak's Problem (that is, $V\left(\tilde{P}\right)=1$ and $\tilde{P}$ minimizes edge length over all polyhedra with unit volume). We therefore seek a polyhedron P which minimizes $\mathcal{F}\left(P\right).$

The problem is mentioned in several sources, most notably as Problem 13 in [M65]. Although not much work has been done to solve the problem, the Regular Triangular Prism is conjectured to be the minimizer. This polyhedron is constructed from three squares and two equilateral triangles:

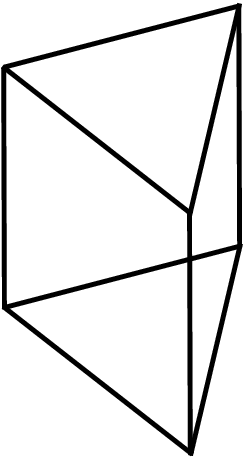
When the edges are chosen to have unit length, then for the Regular Triangular Prism we have $\mathcal{F}\left(RTP\right)=972\sqrt{3}.$ The work contained in [B01] gives evidence to believe that the Regular Triangular Prism is the minimizer.

Known results

First, calculations show that the Regular Triangular Prism has a smaller value of $\mathcal{F}$ than the Platonic Solids . These are the Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron with $\mathcal{F}$ values $1296\sqrt{2},1728,2592\sqrt{2},172800\sqrt{5}{(1+\sqrt{5})}^{-4},$ and $129600{(1+\sqrt{5})}^{-2}$ respectively.

Second, we define a prism to be a polygon in the plane translated in the direction of a vector not in the plane. Then [B01] shows that Right Regular Prisms , prisms formed by translating a polygon with equal sides vertically in the perpendicular direction so that the vertical sides are squares, minimize the value of $\mathcal{F}$ over all prisms. This is done by writing down the formula for the volume of a prism depending on the area of the polygonal base, the height of the prism, and the angle between the base and the generating vector. Given a base, then differentiating this function shows that the volume is minimized, while edge length is preserved, when the generating vector is perpendicular to the base. Then, the 2-Dimensional Isoperimetric Inequality for Polygons shows that the volume can be decreased, while the edge length kept fixed, if the base is regular. Finally, a calculation shows that the Regular Triangular Prism has smallest value of $\mathcal{F}$ amongst all Right Regular Prisms.