| << Chapter < Page | Chapter >> Page > |
In Grade 10 and 11 we focussed on the solution of algebraic equations and excluded equations that dealt with trigonometric functions (i.e. and ). In this section, the solution of trigonometric equations will be discussed.
The methods described in previous Grades also apply here. In most cases, trigonometric identities will be used to simplify equations, before finding the final solution. The final solution can be found either graphically or using inverse trigonometric functions.
As an example, to introduce the methods of solving trigonometric equations, consider
As explained in previous Grades,the solution of Equation [link] is obtained by examining the intersecting points of the graphs of:
Both graphs, for , are shown in [link] and the intersection points of the graphs are shown by the dots.
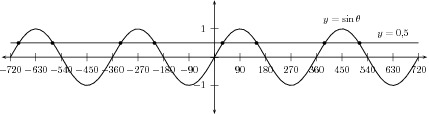
In the domain for of , there are 8 possible solutions for the equation . These are
Find , if , with . Determine the solution graphically.
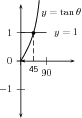
The graphs intersect at
The inverse trigonometric functions , and can also be used to solve trigonometric equations. These may be shown as second functions on your calculator: sin , cos and tan .
Using inverse trigonometric functions, the equation
is solved as
Find , if , with . Determine the solution using inverse trigonometric functions.
Trigonometric equations often look very simple. Consider solving the equation . We can take the inverse sine of both sides to find that . If we put this into a calculator we find that . This is true, however, it does not tell the whole story.
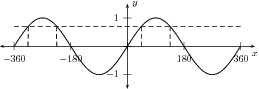
As you can see from [link] , there are four possible angles with a sine of between and . If we were to extend the range of the sine graph to infinity we would in fact see that there are an infinite number of solutions to this equation! This difficulty (which is caused by the periodicity of the sine function) makes solving trigonometric equations much harder than they may seem to be.
Any problem on trigonometric equations will require two pieces of information to solve. The first is the equation itself and the second is the range in which your answers must lie. The hard part is making sure you find all of the possible answers within the range. Your calculator will always give you the smallest answer ( i.e. the one that lies between and for tangent and sine and one between and for cosine). Bearing this in mind we can already solve trigonometric equations within these ranges.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 maths' conversation and receive update notifications?