| << Chapter < Page | Chapter >> Page > |
Verify that is a solution to the differential equation
It is convenient to define characteristics of differential equations that make it easier to talk about them and categorize them. The most basic characteristic of a differential equation is its order.
The order of a differential equation is the highest order of any derivative of the unknown function that appears in the equation.
What is the order of each of the following differential equations?
We already noted that the differential equation has at least two solutions: and The only difference between these two solutions is the last term, which is a constant. What if the last term is a different constant? Will this expression still be a solution to the differential equation? In fact, any function of the form where represents any constant, is a solution as well. The reason is that the derivative of is regardless of the value of It can be shown that any solution of this differential equation must be of the form This is an example of a general solution to a differential equation. A graph of some of these solutions is given in [link] . ( Note : in this graph we used even integer values for ranging between and In fact, there is no restriction on the value of it can be an integer or not.)
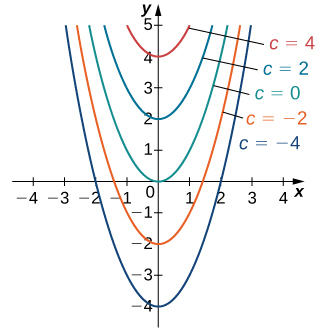
In this example, we are free to choose any solution we wish; for example, is a member of the family of solutions to this differential equation. This is called a particular solution to the differential equation. A particular solution can often be uniquely identified if we are given additional information about the problem.
Find the particular solution to the differential equation passing through the point
Any function of the form is a solution to this differential equation. To determine the value of we substitute the values and into this equation and solve for
Therefore the particular solution passing through the point is
Find the particular solution to the differential equation
passing through the point given that is a general solution to the differential equation.
Usually a given differential equation has an infinite number of solutions, so it is natural to ask which one we want to use. To choose one solution, more information is needed. Some specific information that can be useful is an initial value , which is an ordered pair that is used to find a particular solution.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?