1.1 Standing waves and wind instruments  (Page 4/4)

Displacement waves

Pressure waves

Basic wind instrument tube types

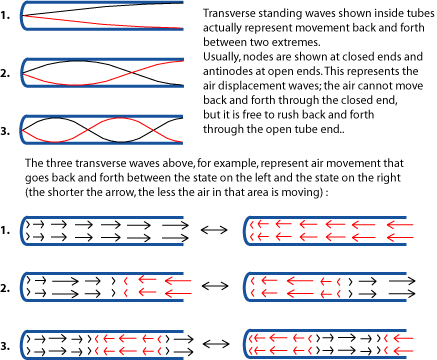
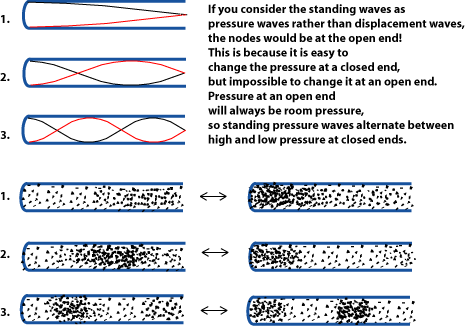
The previous section shows why only the odd-numbered harmonics "fit" in a cylinder-shaped tube, but that is not the whole story. There is one other tube shape that works well for wind instruments, and it abides by slightly different rules.

Just as on a string , the actual wave inside the instrument is a complex wave that includes all of those possible harmonics . A cylinder makes a good musical instrument because all the waves in the tube happen to have simple, harmonic-series-type relationships. This becomes very useful when the player overblows in order to get more notes. As mentioned above, woodwind players get different notes out of their instruments by opening and closing finger holes, making the standing wave tube longer or shorter. Once the player has used all the holes, higher notes are played by overblowing , which causes the next higher harmonic of the tube to sound. In other words, the fundamental of the tube is not heard when the player "overblows"; the note heard is the pitch of the next available harmonic (either harmonic two or three). Brass players can get many different harmonics from their instruments, and so do not need as many fingerings. (Please see Harmonic Series and Wind Instruments – Some Basics for more on this.)

For most possible tube shapes, a new set of holes would be needed to get notes that are in tune with the lower set of notes. But a couple of shapes, including the cylinder, give higher notes that are basically in tune with the lower notes using the same finger holes (or valves). (Even so, some extra finger holes or an extra slide or valve is sometimes necessary for good tuning.) One other possible shape is basically not used because it would be difficult to build precisely and unwieldy to play. (Basically, it has to flare rapidly, at a very specific rate of flare. The resulting instrument would be unwieldy and impractical. Please see John S. Rigden's Physics and the Sound of Music , as cited below for more on this.)

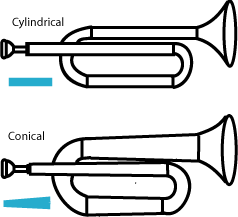
The other tube shape that is often used in wind instruments is the cone. In fact, most real wind instruments are tubes that are some sort of combination of cylindrical and conical tubes. But most can be classified as either cylindrical or conical instruments.

The really surprising thing is that stopped-tube instruments that are basically conical act as if they are open-tube cylindrical instruments.

The clarinet player doesn't have it so easy. Because the clarinet is a very cylindrical instrument, the next harmonic available is three times the frequency, or an octave and a fifth higher, than the fundamental. Extra holes and keys have to be added to the instrument to get the notes in that missing fifth, and then even more keys are added to help the clarinetist get around the awkward fingerings that can ensue. Many notes have several possible fingerings, and the player must choose fingerings based on tuning and ease of motion as they change notes.

So why bother with cylindrical instruments? Remember that an actual note from any instrument is a very complex sound wave that includes lots of harmonics. The pitch that we hear when a wind instrument plays a note is (usually) the lowest harmonic that is being produced in the tube at the time. The higher harmonics produce the timbre , or sound color, of the instrument. A saxophone-shaped instrument simply can't get that odd-harmonics clarinet sound.

The shapes and sounds of the instruments that are popular today are the result of centuries of trial-and-error experimentation by instrument-makers. Some of them understood something of the physics involved, but the actual physics of real instruments - once you add sound holes, valves, keys, mouthpieces, and bells - are incredibly complex, and theoretical physicists are still studying the subject and making new discoveries.

Further reading

• Alexander Wood's The Physics of Music (1944, The Sherwood Press) is a classic which includes both the basics of waves in a pipe and information about specific instruments.
• John Backus' The Acoustical Foundations of Music (1969, W.W. Norton and Company) also goes into more detail on the physics of specific instruments.
• John S. Rigden's Physics and the Sound of Music (1977, John Wiley and Sons) includes most of the math necessary for a really rigorous, complete explanation of basic acoustics, but is (in my opinion) still very readable.
• Arthur H. Benade's Fundamentals of Musical Acoustics is a more technical textbook that gives some idea of how acoustical experiments on instruments are designed and carried out. Those who are less comfortable with the science/engineering aspect of the subject may prefer the two very thorough articles by Benade in:
• The Physics of Music (W. H. Freeman and Co.), a collection of readings from the periodical Scientific American .