| << Chapter < Page | Chapter >> Page > |
What is the voltage across the unknown resistor in the circuit shown?
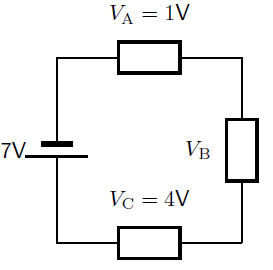
We have a circuit with a battery and three resistors. We know the voltage across the battery and two of the resistors. We want to find that voltage across the unknown resistor.
We know that the voltage across the battery must be equal to the total voltage across all other circuit components that are in series.
The total voltage in the circuit is the sum of the voltages across the individual resistors
Using the relationship between the voltage across the battery and total voltage across the resistors
What is the voltage across the parallel resistor combination in the circuit shown? Hint: the rest of the circuit is the same as the previous problem.
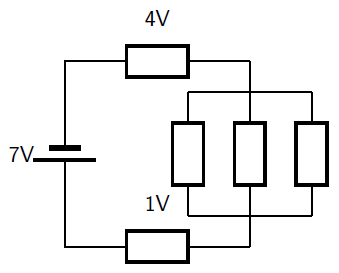
The circuit is the same as the previous example and we know that the voltage difference between two points in a circuit does not depend on what is between them so the answer is the same as above .
We have a circuit with a battery and five resistors (two in series and three in parallel). We know the voltage across the battery and two of the resistors. We want to find that voltage across the parallel resistors, .
We know that the voltage across the battery must be equal to the total voltage across all other circuit components.
Voltages only add for components in series. The resistors in parallel can be thought of as a single component which is in series with the other components and then the voltages can be added.
Using the relationship between the voltage across the battery and total voltage across the resistors
We have been talking about moving charge. But how much charge is moving, and how fast is it moving? The concept that represents this information is called current . Current allows us to quantify the movement of charge.
When we talk about current we talk about how much charge moves past a fixed point in circuit in one second. Think of charges being pushed around the circuit by the battery; there are charges in the wires but unless there is a battery they won't move. When one charge moves, the charges next to it also move. They keep their spacing as if you had a tube of marbles like in this picture.

If you push one marble into the tube then one must come out the other side. If you look at any point in the tube and push one marble into the tube, one marble will move past the point you are looking at. This is similar to charges in the wires of a circuit.
If one charge moves then they all move and the same number move at every point in the circuit. This is due to the conservation of charge.
Now that we've thought about moving charges and visualised what is happening we need to get back to quantifying moving charge. We've already said that we call moving charge current but we define it precisely as follows:

Notification Switch
Would you like to follow the 'Physics - grade 10 [caps 2011]' conversation and receive update notifications?