| << Chapter < Page | Chapter >> Page > |
Rearranging terms we find
Calculation and rounding to 3 significant digits yields the result
Let us ponder a second question based upon the data presented in the original problem.
Question 2 : What is the ground distance traveled by the airplane as it moves from its departure point to its cruise altitude?
Solution : Referring to Figure 2, we observe that we must find the length of the adjacent side in order to answer the question. We can use the definition of the tangent to guide our solution.
Denoting the adjacent side by the symbol A , we obtain
After rounding to 3 significant digits, we obtain the solution
Work is an important concept in virtually every field of science and engineering. It takes work to move an object; it takes work to move an electron through an electric field; it takes work to overcome the force of gravity; etc.
Let’s consider the case where we use an inclined plane to assist in the raising of a 300 pound weight. The inclined plane situated such that one end rests on the ground and the other end rests upon a surface 4 feet aove the ground. This situation is depicted in Figure 3.

Question 3: Suppose that the length of the inclined plane is 12 feet. What is the angle that the plane makes with the ground?
Clearly, the length of the inclined plane is same as that of the hypotenuse shown in the figure. Thus, we may use the sine function to solve for the angle
In order to solve for the angle, we must make use of the inverse sine function as shown below
So we conclude that the inclined plane makes a 19.85 0 angle with the ground.
Neglecting any effects of friction, we wish to determine the amount of work that is expended in moving the block a distance ( L ) along the surface of the inclined plane.
Let us now turn our attention to an example in the field of surveying. In particular, we will investigate how trigonometry can be used to help forest rangers combat fires. Let us suppose that a fire guard observes a fire due south of her Hilltop Lookout location. A second fire guard is on duty at a Watch Tower that is located 11 miles due east of the Hilltop Lookout location. This second guard spots the same fire and measures the bearing (angle) at 215 0 from North. The figure below illustrates the geometry of the situation.

Question: How far away is the fire from the Hilltop Lookout location?
We begin by identifying the angle θ in the figure below.
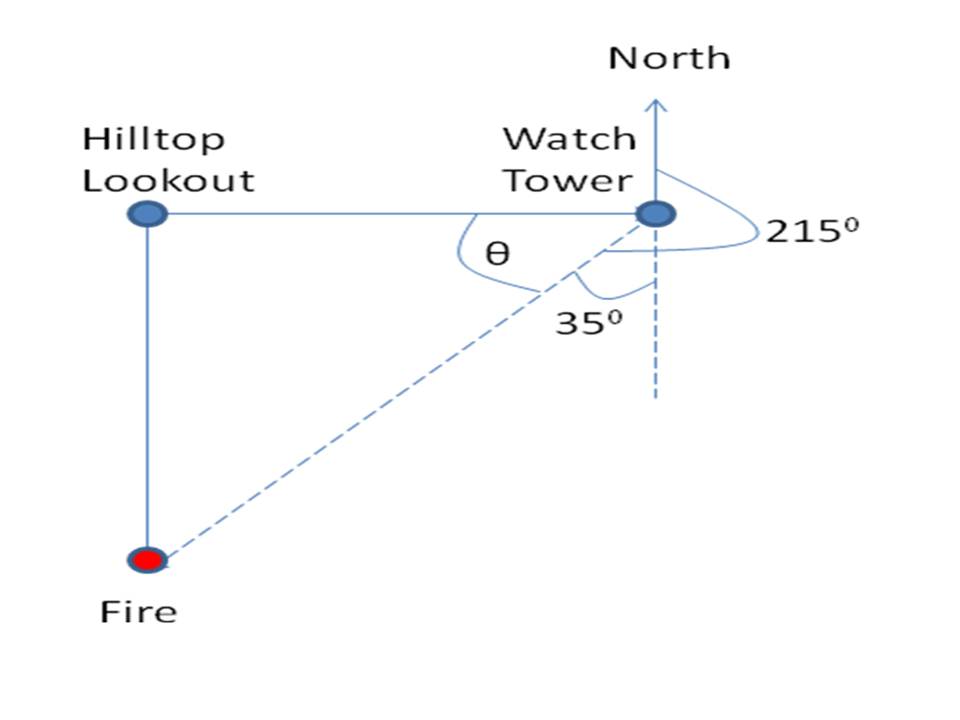
The value of θ can be found via the equation
So we can simplify the drawing as shown below.

Our problem reduces to solving for the value of b .
We conclude that the fire is located 15.7 miles south of the Hilltop Lookout location.
Comment: Triangulation is a process that can be applied to solve problems in a number of areas of engineering including surveying, construction management, radar, sonar, lidar, etc.

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?