9.1 Graphical representation of data

Unlike histograms, many frequency polygons can be plotted together to compare several frequency distributions, provided that the data has been grouped in the same way and provide a clear way to compare multiple datasets.

Pie charts

A pie chart is a graph that is used to show what categories make up a specific section of the data, and what the contribution each category makes to the entire set of data. A pie chart is based on a circle, and each category is represented as a wedge of the circle or alternatively as a slice of the pie. The area of each wedge is proportional to the ratio of that specific category to the total number of data values in the data set. The wedges are usually shown in different colours to make the distinction between the different categories easier.

Method: Drawing a pie-chart

1. Draw a circle that represents the entire data set.
2. Calculate what proportion of 360 ${}^{\circ }$   each category corresponds to according to
   $$\mathrm{Angular}\mathrm{Size}=\frac{\mathrm{Frequency}}{\mathrm{Total}}\times {360}^{\circ }$$
3. Draw a wedge corresponding to the angular contribution.
4. Check that the total degrees for the different wedges adds up to close to ${360}^{\circ }$ .

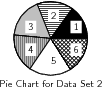
Note that the total angular size of the wedges may not add up to exactly 360 ${}^{\circ }$   because of rounding.

Line and broken line graphs

All graphs that have been studied until this point (bar, compound bar, histogram, frequency polygon and pie) are drawn from grouped data. The graphs that will be studied in this section are drawn from the ungrouped or raw data.

Line and broken line graphs are plots of a dependent variable as a function of an independent variable, e.g. the average global temperature as a function of time, or the average rainfall in a country as a function of season.

Usually a line graph is plotted after a table has been provided showing the relationship between the two variables in the form of pairs. Just as in (x,y) graphs, each of the pairs results in a specific point on the graph, and being a line graph these points are connected to one another by a line.

Many other line graphs exist; they all connect the points by lines, not necessarily straight lines. Sometimes polynomials, for example, are used to describe approximately the basic relationship between the given pairs of variables, and between these points.

Exercises - graphical representation of data

1. Represent the following information on a pie chart.

   Walk	15
   Cycle	24
   Train	18
   Bus	8
   Car	35
   Total	100

   Click here for the solution
2. Represent the following information using a broken line graph.

   Time	07h00	08h00	09h00	10h00	11h00	12h00
   Temp ( ${}^{\circ }$ C)	16	16,5	17	19	20	24

   Click here for the solution
3. Represent the following information on a histogram. Using a coloured pen, draw a frequency polygon on this histogram.

   Time in seconds	Frequency
   16 - 25	5
   26 - 35	10
   36 - 45	26
   46 - 55	30
   56 - 65	15
   66 - 75	12
   76 - 85	10

   Click here for the solution
4. The maths marks of a class of 30 learners are given below, represent this information using a suitable graph.

   82	75	66	54	79	78	29	55	68	91
   43	48	90	61	45	60	82	63	72	53
   51	32	62	42	49	62	81	49	61	60

   Click here for the solution
5. Use a compound bar graph to illustrate the following information

   Year	2003	2004	2005	2006	2007
   Girls	18	15	13	12	15
   Boys	15	11	18	16	10

   Click here for the solution