1.15 Game 2302-0145: getting started with the vector dot product  (Page 20/20)

Exercises

Exercise 1

Using Java and the game-math library named GM02 , or using a different programming environment of your choice, write a program that behavesas follows.

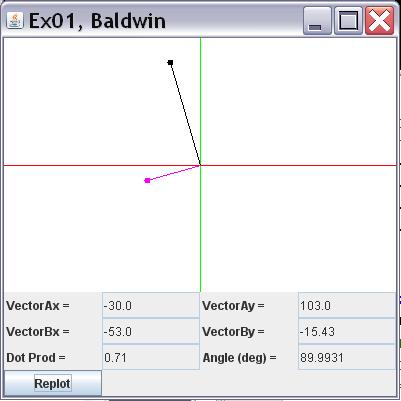
When the program starts running, an image similar to Figure 17 appears on the screen. Each of the text fields is blank and the drawing area at the top is also blank.

Each time you click the Replot button, the program generates three random values in the general range of -128 to 127. The first two valuesare used as the x and y values for a vector. The two values are displayed in the fields labeled VectorAx and VectorAy . Also, the two values are used to create and draw a black vector with its tail at the origin asshown in Figure 17 .

The third random value is used as the x-value for a second vector. It is displayed in the field labeled VectorBx . A y-value is computed that will cause that vector to be perpendicular to the black vector. That valueis displayed in the field labeled VectorBy and the two values are used to draw the magenta vector shown in Figure 17 .

The dot product between the two vectors is computed and displayed in the field labeled Dot Prod . The angle between the two vectors is computed and displayed in the field labeled Angle (deg) .

If the two vectors are perpendicular, the dot product should be close to zero and the angle should be very closeto 90 degrees.

Cause your name to appear in the screen output in some manner.

Figure 17 Output from Exercise 1.

Exercise 2

Using Java and the game-math library named GM02 , or using a different programming environment of your choice, write a program that behavesas follows.

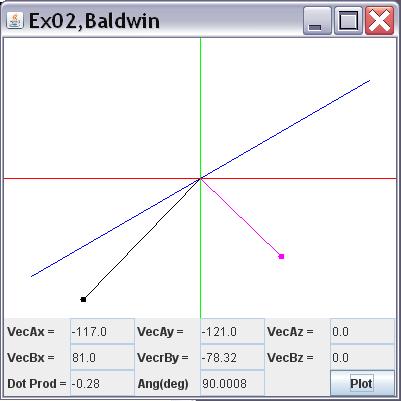
When the program starts running, an image similar to Figure 18 appears on the screen. Each of the text fields is blank and the drawing area at the top is also blank.

Each time you click the Plot button, the program generates three random values in the general range of -128 to 127. The first two valuesare used as the x and y values for a 3D vector. (Set the z-value for the vector to 0.0.) The three values are displayed inthe fields labeled VecAx , VecAy , and VecAz . Also, the three values are used to create and draw a black 3D vector with its tail atthe origin as shown in Figure 18 .

The third random value is used as the x value for a second 3D vector. (Set the z-value for the vector to 0.0.) Those two values are displayed in the fields labeled VecBx and VecBz . A y-value is computedthat will cause that vector to be perpendicular to the black vector. That value is displayed in the field labeled VecBy and the three values are used to draw the magenta vector shown in Figure 18 .

The dot product between the two vectors is computed and displayed in the field labeled Dot Prod . The angle between the two vectors is computed and displayed in the field labeled Angle (deg) .

If the two vectors are perpendicular, the dot product should be close to zero and the angle should be very closeto 90 degrees.

Cause your name to appear in the screen output in some manner.

Figure 18 Output from Exercise 2.

Exercise 3

Using Java and the game-math library named GM02 , or using a different programming environment of your choice, write a program that behavesas follows.

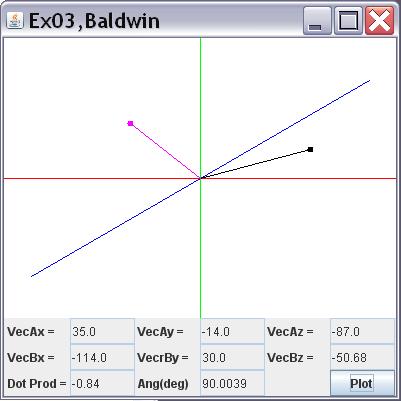
When the program starts running, an image similar to Figure 19 appears on the screen. Each of the text fields is blank and the drawing area at the top is also blank.

Each time you click the Plot button, the program generates five random values in the general range of -128 to 127. The first three valuesare used as the x, y, and z values for a vector. The three values are displayed in the fields labeled VecAx , VecAy , and VecAz . Also, the three values are used to create and draw a black vector with its tail atthe origin as shown in Figure 19 .

The fourth and fifth random values are used as the x and y values for a second vector. They are displayed in the fields labeled VecBx and VecBy . A z-value is computedthat will cause that vector to be perpendicular to the black vector. That value is displayed in the field labeled VecBz and the three values are used to draw the magenta vector shown in Figure 19 .

The dot product between the two vectors is computed and displayed in the field labeled Dot Prod . The angle between the two vectors is computed and displayed in the field labeled Angle (deg) .

If the two vectors are perpendicular, the dot product should be close to zero and the angle should be very closeto 90 degrees.

Cause your name to appear in the screen output in some manner.

Figure 19 Output from Exercise 3.

-end-