| << Chapter < Page | Chapter >> Page > |
Each pair can be represented by a wavefunction of the form
![]()
where P is the net momentum of the pair whose center of mass is at r . However, all the Cooper pairs in a superconductor can be described by a single wavefunction yet again due to the fact that the electrons are in a Coopers pair state and are thus Bosons in the absence of a current because all the pairs have the same phase - they are said to be "phase coherent"
![]()
This electron-pair wave retains its phase coherence over long distances, and essentially produces a standing wave over the device circuit. In a SQUID there are two paths which form a circle and are made with the same standing wave ( [link] ). The wave is split in two sent off along different paths, and then recombined to record an interference pattern by adding the difference between the two.
This allows measurement at any phase differences between the two components, which if there is no interference will be exactly the same, but if there is a difference in their path lengths or in some interaction that the waves encounters such as a magnetic field it will correspond in a phase difference at the end of each path length.
A good example to use is of two water waves emanating from the same point. They will stay in phase if they travel the same distance, but will fall out of phase if one of them has to deviate around an obstruction such as a rock. Measuring the phase difference between the two waves then provides information about the obstruction.
Another implication of this long range coherence is the ability to calculate phase and amplitude at any point on the wave's path from the knowledge of its phase and amplitude at any single point, combined with its wavelength and frequency. The wavefunction of the electron-pair wave in the above eqn. can be rewritten in the form of a one-dimensional wave as
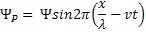
If we take the wave frequency, V , as being related to the kinetic energy of the Cooper pair with a wavelength, λ , being related to the momentum of the pair by the relation λ = h/p then it is possible to evaluate the phase difference between two points in a current carrying superconductor.
If a resistanceless current flows between points X and Y on a superconductor there will be a phase difference between these points that is constant in time.
The parameters of a standing wave are dependent on a current passing through the circuit; they are also strongly affected by an applied magnetic field. In the presence of a magnetic field the momentum, p , of a particle with charge q in the presence of a magnetic field becomes m V + q A where A is the magnetic vector potential. For electron-pairs in an applied field their moment P is now equal to 2mV+2eA .
In an applied magnetic field the phase difference between points X and Y is now a combination of that due to the supercurrent and that due to the applied field.
One effect of the long range phase coherence is the quantization of magnetic flux in a superconducting ring. This can either be a ring, or a superconductor surrounding a non-superconducting region. Such an arrangement can be seen in [link] where region N has a flux density B within it due to supercurrents flowing around it in the superconducting region S .

Notification Switch
Would you like to follow the 'The cat's meow' conversation and receive update notifications?