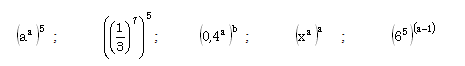Mathematics
Grade 9
Numbers
Module 2
Easier algebra with exponents
Easier algebra with exponents
CLASS WORK
Do you remember how exponents work? Write down the meaning of “three to the power seven”. What is the base? What is the exponent? Can you explain clearly what a power is?
In this section you will find many numerical examples; use your calculator to work through them to develop confidence in the methods.
1 DEFINITION
2
3 = 2 × 2 × 2 and a
4 = a × a × a × a and b × b × b = b
3
also
(a+b)
3 = (a+b) × (a+b) × (a+b) and
2
3
4
=
2
3
×
2
3
×
2
3
×
2
3
size 12{ left ( { {2} over {3} } right ) rSup { size 8{4} } = left ( { {2} over {3} } right ) times left ( { {2} over {3} } right ) times left ( { {2} over {3} } right ) times left ( { {2} over {3} } right )} {}
1.1 Write the following expressions in expanded form:
4
3 ; (p+2)
5 ; a
1 ; (0,5)
7 ; b
2 × b
3 ;
1.2 Write these expressions as powers:
7 × 7 × 7 × 7
y × y × y × y × y
–2 × –2 × –2
(x+y) × (x+y) × (x+y) × (x+y)
1.3 Answer without calculating: Is (–7)
6 the same as –7
6 ?
Now use your calculator to check whether they are the same.
Compare the following pairs, but first guess the answer before using your calculator to see how good your estimate was.
–5
2 and (–5)
2 –12
5 and (–12)
5 –1
3 and (–1)
3
By now you should have a good idea how brackets influence your calculations – write it down carefully to help you remember to use it when the problems become harder.
a
r = a × a × a × a × . . . (There must be r a’s, and r must be a natural number)
It is good time to start memorising the most useful powers:
2
2 = 4; 2
3 = 8; 2
4 = 16; etc. 3
2 = 9; 3
3 = 27; 3
4 = 81; etc. 4
2 = 16; 4
3 = 64; etc.
Most problems with exponents have to be done without a calculator!
2 MULTIPLICATION
Do you remember that g
3 × g
8 = g
11 ? Important words:
multiply ;
same base
2.1 Simplify: (don’t use expanded form)
7
7 × 7
7
(–2)
4 × (–2)
13
( ½ )
1 × ( ½ )
2 × ( ½ )
3
(a+b)
a × (a+b)
b
We multiply powers with the same base according to this rule:
a
x × a
y = a
x+y
also
a
x
+
y
=
a
x
×
a
y
=
a
y
×
a
x
size 12{a rSup { size 8{x+y} } =a rSup { size 8{x} } times a rSup { size 8{y} } =a rSup { size 8{y} } times a rSup { size 8{x} } } {} , e.g.
8
14
=
8
4
×
8
10
size 12{8 rSup { size 8{"14"} } =8 rSup { size 8{4} } times 8 rSup { size 8{"10"} } } {}
3 DIVISION
4
6
4
2
=
4
6
−
2
=
4
4
size 12{ { {4 rSup { size 8{6} } } over {4 rSup { size 8{2} } } } =4 rSup { size 8{6 - 2} } =4 rSup { size 8{4} } } {} is how it works. Important words:
divide ;
same base
3.1 Try these:
a
6
a
y
size 12{ { {a rSup { size 8{6} } } over {a rSup { size 8{y} } } } } {} ;
3
23
3
21
size 12{ { {3 rSup { size 8{"23"} } } over {3 rSup { size 8{"21"} } } } } {} ;
a
+
b
p
a
+
b
12
size 12{ { { left (a+b right ) rSup { size 8{p} } } over { left (a+b right ) rSup { size 8{"12"} } } } } {} ;
a
7
a
7
size 12{ { {a rSup { size 8{7} } } over {a rSup { size 8{7} } } } } {}
The rule for dividing powers is:
a
x
a
y
=
a
x
−
y
size 12{ { {a rSup { size 8{x} } } over {a rSup { size 8{y} } } } =a rSup { size 8{x - y} } } {} .
Also
a
x
−
y
=
a
x
a
y
size 12{a rSup { size 8{x - y} } = { {a rSup { size 8{x} } } over {a rSup { size 8{y} } } } } {} , e.g.
a
7
=
a
20
a
13
size 12{a rSup { size 8{7} } = { {a rSup { size 8{"20"} } } over {a rSup { size 8{"13"} } } } } {}
4 RAISING A POWER TO A POWER
e.g.
3
2
4
size 12{ left (3 rSup { size 8{2} } right ) rSup { size 8{4} } } {} =
3
2
×
4
size 12{3 rSup { size 8{2 times 4} } } {} =
3
8
size 12{3 rSup { size 8{8} } } {} .
4.1 Do the following:
This is the rule:
a
x
y
=
a
xy
size 12{ left (a rSup { size 8{x} } right ) rSup { size 8{y} } =a rSup { size 8{ ital "xy"} } } {}
also
a
xy
=
a
x
y
=
a
y
x
size 12{a rSup { size 8{ ital "xy"} } = left (a rSup { size 8{x} } right ) rSup { size 8{y} } = left (a rSup { size 8{y} } right ) rSup { size 8{x} } } {} , e.g.
6
18
=
6
6
3
size 12{6 rSup { size 8{"18"} } = left (6 rSup { size 8{6} } right ) rSup { size 8{3} } } {}
5 THE POWER OF A PRODUCT
(2a)
3 = (2a) × (2a) × (2a) = 2 × a × 2 × a × 2 × a = 2 × 2 × 2 × a × a × a = 8a
3
It is usually done in two steps, like this: (2a)
3 = 2
3 × a
3 = 8a
3
5.1 Do these yourself: (4x)
2 ; (ab)
6 ; (3 × 2)
4 ; ( ½ x)
2 ; (a
2 b
3 )
2
It must be clear to you that the exponent belongs to each factor in the brackets.
The rule: (ab)
x = a
x b
x
also
a
p
×
b
p
=
ab
b
size 12{a rSup { size 8{p} } times b rSup { size 8{p} } = left ( ital "ab" right ) rSup { size 8{b} } } {} e.g.
14
3
=
2
×
7
3
=
2
3
7
3
size 12{"14" rSup { size 8{3} } = left (2 times 7 right ) rSup { size 8{3} } =2 rSup { size 8{3} } 7 rSup { size 8{3} } } {}
and
3
2
×
4
2
=
3
×
4
2
=
12
2
size 12{3 rSup { size 8{2} } times 4 rSup { size 8{2} } = left (3 times 4 right ) rSup { size 8{2} } ="12" rSup { size 8{2} } } {}
6 A POWER OF A FRACTION
This is much the same as the power of a product.
a
b
3
=
a
3
b
3
size 12{ left ( { {a} over {b} } right ) rSup { size 8{3} } = { {a rSup { size 8{3} } } over {b rSup { size 8{3} } } } } {}
6.1 Do these, but be careful:
2
3
p
size 12{ left ( { {2} over {3} } right ) rSup { size 8{p} } } {}
−
2
2
3
size 12{ left ( { { left ( - 2 right )} over {2} } right ) rSup { size 8{3} } } {}
x
2
y
3
2
size 12{ left ( { {x rSup { size 8{2} } } over {y rSup { size 8{3} } } } right ) rSup { size 8{2} } } {}
a
−
x
b
−
y
−
2
size 12{ left ( { {a rSup { size 8{ - x} } } over {b rSup { size 8{ - y} } } } right ) rSup { size 8{ - 2} } } {}
Again, the exponent belongs to both the numerator and the denominator.
The rule:
a
b
m
=
a
m
b
m
size 12{ left ( { {a} over {b} } right ) rSup { size 8{m} } = { {a rSup { size 8{m} } } over {b rSup { size 8{m} } } } } {}
and
a
m
b
m
=
a
b
m
size 12{ { {a rSup { size 8{m} } } over {b rSup { size 8{m} } } } = left ( { {a} over {b} } right ) rSup { size 8{m} } } {} e.g.
2
3
3
=
2
3
3
3
=
8
27
size 12{ left ( { {2} over {3} } right ) rSup { size 8{3} } = { {2 rSup { size 8{3} } } over {3 rSup { size 8{3} } } } = { {8} over {"27"} } } {}
and
a
2x
b
x
=
a
2
x
b
x
=
a
2
b
x
size 12{ { {a rSup { size 8{2x} } } over {b rSup { size 8{x} } } } = { { left (a rSup { size 8{2} } right ) rSup { size 8{x} } } over {b rSup { size 8{x} } } } = left ( { {a rSup { size 8{2} } } over {b} } right ) rSup { size 8{x} } } {}
end of CLASS WORK
TUTORIAL
Apply the rules together to simplify these expressions without a calculator.
1.
a
5
×
a
7
a
×
a
8
size 12{ { {a rSup { size 8{5} } times a rSup { size 8{7} } } over {a times a rSup { size 8{8} } } } } {} 2.
x
3
×
y
4
×
x
2
y
5
x
4
y
8
size 12{ { {x rSup { size 8{3} } times y rSup { size 8{4} } times x rSup { size 8{2} } y rSup { size 8{5} } } over {x rSup { size 8{4} } y rSup { size 8{8} } } } } {}
3.
a
2
b
3
c
2
×
ac
2
2
×
bc
2
size 12{ left (a rSup { size 8{2} } b rSup { size 8{3} } c right ) rSup { size 8{2} } times left ( ital "ac" rSup { size 8{2} } right ) rSup { size 8{2} } times left ( ital "bc" right ) rSup { size 8{2} } } {} 4.
a
3
×
b
2
×
a
3
a
×
b
5
b
4
×
ab
3
size 12{a rSup { size 8{3} } times b rSup { size 8{2} } times { {a rSup { size 8{3} } } over {a} } times { {b rSup { size 8{5} } } over {b rSup { size 8{4} } } } times left ( ital "ab" right ) rSup { size 8{3} } } {}
5.
2
xy
×
2x
2
y
4
2
×
x
2
y
3
2
xy
3
size 12{ left (2 ital "xy" right ) times left (2x rSup { size 8{2} } y rSup { size 8{4} } right ) rSup { size 8{2} } times left ( { { left (x rSup { size 8{2} } y right ) rSup { size 8{3} } } over { left (2 ital "xy" right ) rSup { size 8{3} } } } right )} {} 6.
2
3
×
2
2
×
2
7
8
×
4
×
8
×
2
×
8
size 12{ { {2 rSup { size 8{3} } times 2 rSup { size 8{2} } times 2 rSup { size 8{7} } } over {8 times 4 times 8 times 2 times 8} } } {}
end of TUTORIAL
Some more rules
CLASS WORK
1 Consider this case:
a
5
a
3
=
a
5
−
3
=
a
2
size 12{ { {a rSup { size 8{5} } } over {a rSup { size 8{3} } } } =a rSup { size 8{5 - 3} } =a rSup { size 8{2} } } {}