| << Chapter < Page | Chapter >> Page > |
Another example of energy conversion occurs in a solar cell. Sunlight impinging on a solar cell (see [link] ) produces electricity, which in turn can be used to run an electric motor. Energy is converted from the primary source of solar energy into electrical energy and then into mechanical energy.

| Object/phenomenon | Energy in joules |
|---|---|
| Big Bang | |
| Energy released in a supernova | |
| Fusion of all the hydrogen in Earth’s oceans | |
| Annual world energy use | |
| Large fusion bomb (9 megaton) | |
| 1 kg hydrogen (fusion to helium) | |
| 1 kg uranium (nuclear fission) | |
| Hiroshima-size fission bomb (10 kiloton) | |
| 90,000-ton aircraft carrier at 30 knots | |
| 1 barrel crude oil | |
| 1 ton TNT | |
| 1 gallon of gasoline | |
| Daily home electricity use (developed countries) | |
| Daily adult food intake (recommended) | |
| 1000-kg car at 90 km/h | |
| 1 g fat (9.3 kcal) | |
| ATP hydrolysis reaction | |
| 1 g carbohydrate (4.1 kcal) | |
| 1 g protein (4.1 kcal) | |
| Tennis ball at 100 km/h | |
| Mosquito | |
| Single electron in a TV tube beam | |
| Energy to break one DNA strand |
Even though energy is conserved in an energy conversion process, the output of useful energy or work will be less than the energy input. The efficiency of an energy conversion process is defined as
[link] lists some efficiencies of mechanical devices and human activities. In a coal-fired power plant, for example, about 40% of the chemical energy in the coal becomes useful electrical energy. The other 60% transforms into other (perhaps less useful) energy forms, such as thermal energy, which is then released to the environment through combustion gases and cooling towers.
| Activity/device | Efficiency (%) Representative values |
|---|---|
| Cycling and climbing | 20 |
| Swimming, surface | 2 |
| Swimming, submerged | 4 |
| Shoveling | 3 |
| Weightlifting | 9 |
| Steam engine | 17 |
| Gasoline engine | 30 |
| Diesel engine | 35 |
| Nuclear power plant | 35 |
| Coal power plant | 42 |
| Electric motor | 98 |
| Compact fluorescent light | 20 |
| Gas heater (residential) | 90 |
| Solar cell | 10 |
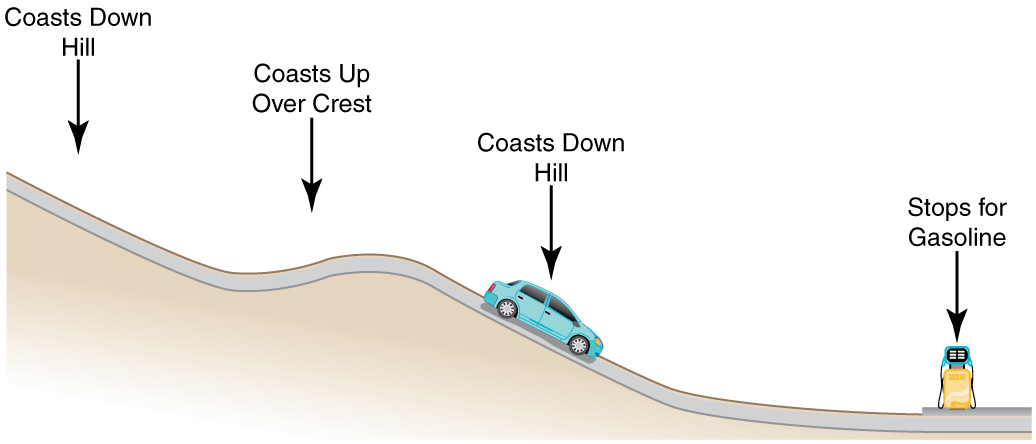
Consider the following scenario. A car for which friction is not negligible accelerates from rest down a hill, running out of gasoline after a short distance. The driver lets the car coast farther down the hill, then up and over a small crest. He then coasts down that hill into a gas station, where he brakes to a stop and fills the tank with gasoline. Identify the forms of energy the car has, and how they are changed and transferred in this series of events. (See [link] .)
Do devices with efficiencies of less than one violate the law of conservation of energy? Explain.
List the energy conversions that occur when riding a bicycle.
Using energy considerations and assuming negligible air resistance, show that a rock thrown from a bridge 20.0 m above water with an initial speed of 15.0 m/s strikes the water with a speed of 24.8 m/s independent of the direction thrown.
Equating and , we obtain

Notification Switch
Would you like to follow the 'Unit 5 - work and energy' conversation and receive update notifications?